Zašto je funkcija raspodele važna? Ako nju znamo, možemo za svaki interval da odredimo verovatnoću da slućajna promenljiva uzme neku od vrednosti iz tog intervala.
P{a ≤ X ≤ b} = P{X ≤ b} - P{a ≤ X} = Fx (b) – Fx(a)
Funkcija raspodele FX slučajne promenljive X je neopadajuća funkcija , neprekidna sa desne strane i za nju važi: F (−∞) = 0 i F (∞) = 1.
Za diskretnu slučajnu promenljivu X skup {p(xk) | xk ∈ X(S)} određuje raspodelu verovatnoća slučajne promenljive X. Ova raspodela se pregledno prikazuje šemom:
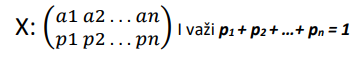
Primer: Ako bacimo kockicu skup ishoda će biti Ω={1,2,3,4,5}. Verovatnoća da padne svaki od tih brojeva je p=1/6. Ako sa X označimo slučajnu promenljivu koja predstavlja ishod eskperimenta, to će biti diskretna slučajna promenljiva i rasodela verovatnoca izgleda ovako:
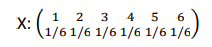
Ako je X diskretna slućajna promenljiva sa konačno mnogo vrednosti {x1, x2, . . . , xn}, tada je njena funkcija raspodele zadata sa:
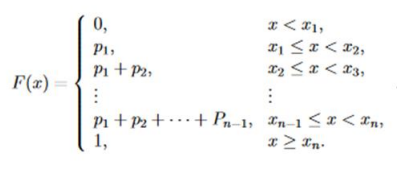
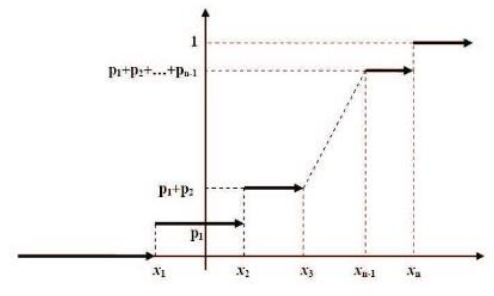
Na sledećoj slici se vidi da je grafik funkcije raspodele diskretne slučajne promenljive stepenastog oblika:
Primer: Ako slučajna promenljiva X ima sledeći zakon raspodele:
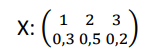
Njena funkcija raspodele je:
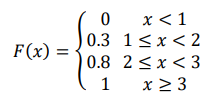
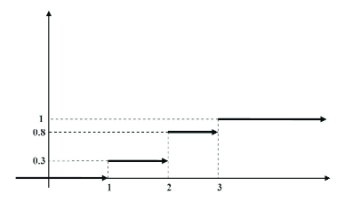
Za slučajnu promenljivu X kažemo da je apsolutno neprekidnog tipa ako postoji nenegativna integrabilna funkcija p(x) na intervalu (-∞,x), x∈ R , takva da je:
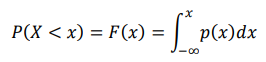
Funkcija p naziva se gustina raspodele slučajne promenljive X. Grafik funkcije p(x) naziva se kriva gustine raspodele ili kraće kriva raspodele verovatnoća.
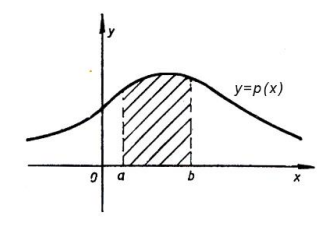
Geometrijski posmatrano, F(x), verovatnoća da slučajna promenljiva X uzme vrednost manju od x, jednaka površini figure omeđene krivom gustine (grafikom p(x)) i X-osom nad intervalom (-∞, x).
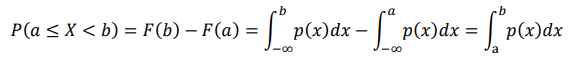
Verovatnoća da slučajna promenljiva apsolutno neprekidnog tipa uzme vrednost u intervalu (a,b) jednaka je površini krivolinijskog trapeza ispod krive gustine (y=p(x)) nad odsečkom [a,b].
Primer: Za funkciju:
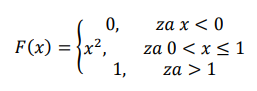
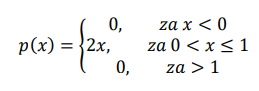
_____________________________________________________________________________________________
Zadaci:
1. U kutiji se nalaze 3 kuglice numerisane brojevima 1,2,3. Na slučajan način se biraju 2 kuglice, jedna po jedna sa vraćanjem. Ako slučajna vrednost X predstavlja količnik brojeva dobijenih u prvom i drugom bacanju odrediti njenu raspodelu verovatnoće i odrediti verovatnoću da X ima celobrojnu vrednost.
Rešenje se nalazi na sledećem linku.
2. Slučajna veličina Z ima sledeći zakon raspodele:
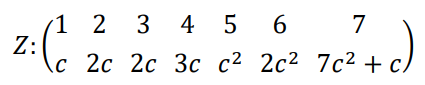
a. Odrediti vrednost konstante c
b. Izračunati verovatnoću da će se Z naći između 2 i 5
c. Odrediti najmanje k tako da je verovatnoća da je Z≤k veća od 0, 6.
Rešenje:
- a. Vrednost konstante c dobijamo iz jednačine
- 𝑐 + 2𝑐 + 2𝑐 + 3𝑐 + c2 + 2c2 + 7c2 + 𝑐 = 1
- Kada rešimo kvadratnu jednačinu, dobijemo da c može da ima vrednost c1 = -1 ili c2 = 1/10.
Rešenje c1=-1 otpada, jer c ∈ (0,1). Iz toga sledi da je vrednost konstante c = 1/10.
- b. Verovatnoća da se Z nađe između 2 i 5 je:
- 𝑃{2 < 𝑍 < 5} = 𝑃 {𝑍 = 3} + 𝑃 {𝑍 = 4} = 2 ∗ 𝑐 + 3 ∗ 𝑐 = 1/2
- c. Računamo funkciju raspodele u tačkama 1,2,3,..7.
- 𝑃{𝑍 < 1} =1/10 < 0.6
- 𝑃{𝑍 < 2} = 1/10 +2/10 = 3/10 < 0.6
- 𝑃{𝑍 < 3} =1/10 +2/10 +2/10 =5/10 < 0.6
- 𝑃{𝑍 < 4} =1/10 +2/10 +2/10 +3/10 =8/10 > 0.6
- Iz ovoga zaključujemo da je najmanje k koje ispunjava dati uslov k=4.