Procesi  Markova i primene

Uvod

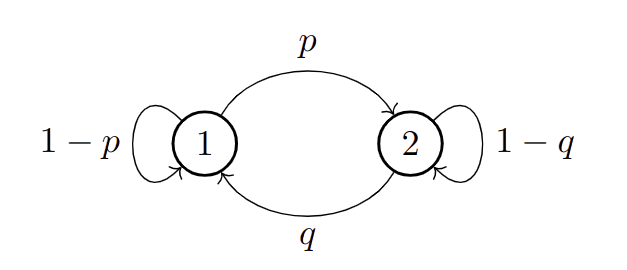
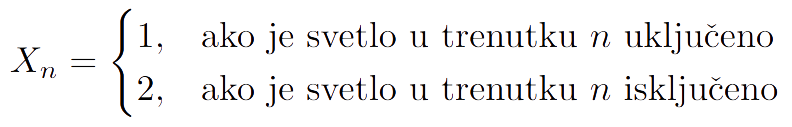Za praćenje kursa pretpostavlja se poznavanje osnovnih pojmova teorije verovatnoće, kao što su: verovatnoća, slučajni događaj, prostor verovatnoća i slučajna veličina.

Osnovni pojam za naš kurs je slučajni proces. Slučajni proces je skup slučajnih veličina {X t |t∈T} definisanih na istom prostoru verovatnoća, pri čemu je T beskonačan skup.

T je parametarski skup. Parametarski skup možemo da interpretiramo i kao vreme (tako ga i zovemo).

Ako je parametarski skup diskretan, onda taj slučajni proces zovemo slučajni proces sa diskretnim parametrom (slučajni niz), a ako je parametarski skup neprekidan, to zovemo slučajni proces sa neprekidnim parametrom.

Primeri slučajnih procesa:

  1. Temperatura na nekom mestu merena svakog sata (temperatura u ovom slučaju predstavlja slučajnu veličinu, a sati parametarski skup)
  2. Broj primljenih telefonskih poziva od početka registrovanja do trenutka t (sama slučajna veličina je diskretna (broj poziva), a svakom trenutku možemo proveriti koliko je poziva stiglo, pa je parametarski skup neprekidan)
  3. Kretanje cene akcije na berzi od nekog početnog trenutka do trenutka t (ovde je i slučajna veličina i vreme neprekidno).

Specijalna vrsta slučajnih procesa, koju zov​emo procesi Markova, može se jednostavno opisati ovako: "budućnost procesa zavisi samo od sadašnjosti (ili poslednjeg registrovanog trenutka), a ne i od prošlosti".
Šta znači ovaj opis objasnićemo na sledećem primeru: 

Svetlo u prostoriji može biti uključeno ili isključeno. Svakog sata neka osoba ulazi u prostoriju. Ako vidi uključeno svetlo, osoba ga isključuje sa verovatnoćom p , a ostavlja uključenim sa verovatnoćom 1 − p . Ako osoba vidi isključeno svetlo, ona ga uključuje sa verovatnoćom q , ili ostavlja isključenim sa verovatnoćom 1 − q . Zaključujemo da svetlo u sobi u trenutku n + 1 (posle n + 1 sati) zavisi samo od stanja svetla u trenutku n (posle n sati) i od toga da li će ga ta osoba isključiti ili uključiti (a ne zavisi od toga šta se desilo u prethodnih n − 1 trenutaka (sati)). To znači, da sva prethodna dešavanja vezana za uključivanje i isključivanje svetla nisu bitna, pa možemo da ih zaboravimo. Ovo svojstvo, inače veoma važno i korisno, zovemo svojstvo Markova. Takođe, možemo da primetimo da, ako zapišemo dešavanja vezana za svetlo u prostoriji na sledeći način:

onda je {X n |n ∈ ℕ} jedan slučajni niz koji može da uzme samo dve moguće vrednosti, tj. možemo da kažemo da se nalazi u dva stanja. Pri tome, nije bitno da li ćemo ta stanja obeležavati sa 1 i 2, sa "on" i "off" (ili nekako drugačije), već je samo bitno da znamo koliko ih tačno ima i sa kojim verovatnoćama se iz jednog od njih prelazi u drugo. Sve to možemo prikazati i na sledeći način:

Na ovoj slici kružići predstavljaju stanja u kojima se može naći ovaj slučajni niz, a strelice predstavljaju prelaske iz jednog stanja u drugo (uključujući i mogućnost ostajanja u istom stanju). Pored svake strelice je zapisana verovatnoća odgovarajućeg prelaza. I drugi procesi Markova se mogu prikazati na ovaj način.

Procesi Markova mogu imati diskretan i neprekidan parametarski skup, tj. mogu biti ,,u diskretnom vremenu” ili ,,u neprekidnom vremenu”.

Procesi Markova sa diskretnim vremenom Procesi Markova sa neprekidnim vremenom
Website Templates

created with

Website Builder Software .