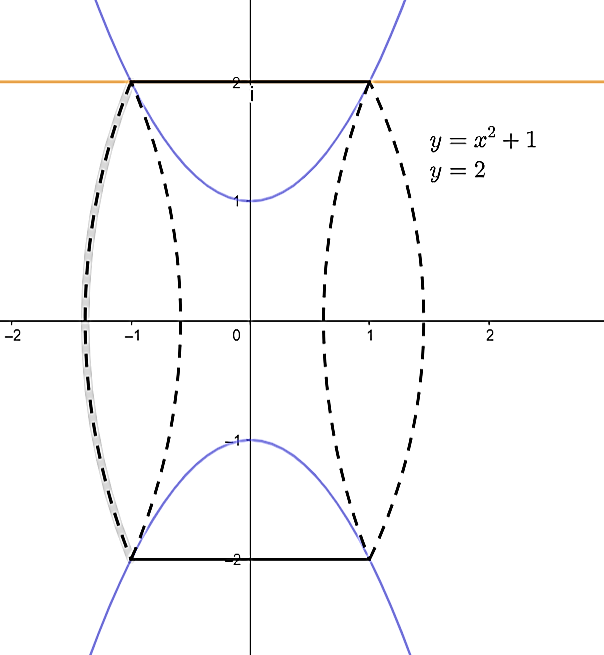
Задатак 1. Наћи запремину тела добијеног ротацијом око `x`-осе фигуре ограничене кривама \[ y=x^2+1 \quad и\quad y=2.\]
Решење. Укупну запремину добијамо разликом запремина насталих тела ротацијом: \[V=V_1-V_2.\] Решавамо систем, да бисмо добили границе:
\[ \left.\ \begin{matrix}y=x^2+1\\y=2\\\end{matrix}\right\}\ \Longrightarrow\ 2=x^2+1\ \Longrightarrow\ x^2-1=0\ \Longrightarrow\ \left(x-1\right)\left(x+1\right)=0\Longrightarrow\ x=1\land\ x=-1; \]
Затим рачунамо појединачно запремине `V_1 и V_2`: \[V_1=\pi∫_{-1}^12^2dx=4πx|_{-1}^1=4π(1+1)=8π;\] \[V_2=π∫_{-1}^1(x^2+1)^2dx=π∫_{-1}^1(x^4+2x^2+1)dx=π[\frac{x^5}{5}+\frac{2x^3}{3}+x]|_{-1}^1=\ \pi\left(\frac{1}{5}+\frac{2}{3}+1+\frac{1}{5}+\frac{2}{3}+1\right)=\frac{56}{15}\pi.\]
Крајње решење: \[ V=V_1-V_2=8\pi-\frac{56}{15}\pi=\frac{64}{15}\pi.\]
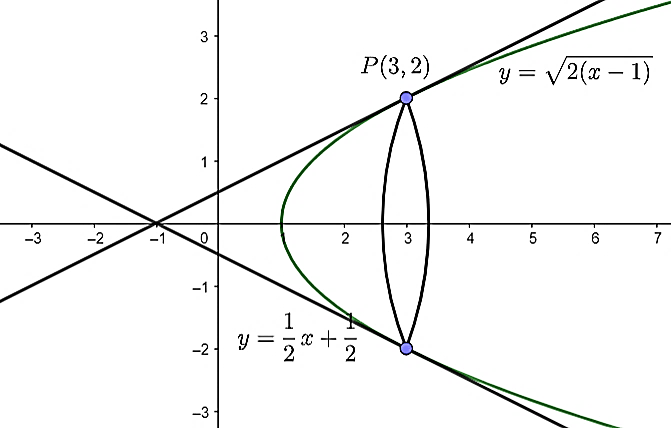
Задатак 2. У тачки `P(3,2)` криве `y^2=2(x-1)` конструисана је тангента. Израчунати запремину тела које настаје ротацијом око `x`-осе фигуре ограничене овом тангентом датом кривом и `x`-осом.
Решење. Укупну запремину добијамо разликом запремина насталих тела ротацијом: \[V=V_1-V_2.\]
\[ \left.\ \begin{matrix}y=x^2+1\\y=2\\\end{matrix}\right\}\ \Longrightarrow\ 2=x^2+1\ \Longrightarrow\ x^2-1=0\ \Longrightarrow\ \left(x-1\right)\left(x+1\right)=0\Longrightarrow\ x=1\land\ x=-1; \]
Затим рачунамо појединачно запремине `V_1 и V_2`: \[V_1=\pi∫_{-1}^3(\frac{1}{2}x+\frac{1}{2})^2dx=π∫_{-1}^3(\frac{1}{4}x^2+\frac{1}{2}x+\frac{1}{4})dx= π∫_{-1}^3\frac{1}{4}x^2dx+π∫_{-1}^3\frac{1}{2}xdx+π∫_{-1}^3\frac{1}{4}dx=\] \[\frac{1}{4}π\frac{x^3}{3}|_{-1}^3+\frac{1}{2}π\frac{x^2}{2}|_{-1}^3+\frac{1}{4}πx|_{-1}^3=\frac{π}{4}\frac{28}{3}+\frac{π}{2}\frac{8}{2}+\frac{π}{4}⋅4=73π+2π+π=163π.\] \[V_2=π∫_{-1}^1(x^2+1)^2dx=π∫_{-1}^1(x^4+2x^2+1)dx=π[\frac{x^5}{5}+\frac{2x^3}{3}+x]|_{-1}^1=\ \pi\left(\frac{1}{5}+\frac{2}{3}+1+\frac{1}{5}+\frac{2}{3}+1\right)=\frac{56}{15}\pi.\]
Крајње решење: \[ V=V_1-V_2=\frac{16\pi}{3}-4\pi=\frac{4\pi}{3}.\]
Једначина тангенте: \[t:\ \ \ \ y-2=k(x-3);\]
\[t:y-2=\frac{1}{2}x-\frac{3}{2}\ \Longrightarrow\ t:y=\frac{1}{2}x+\frac{1}{2}\Rightarrow\ y=0\Rightarrow\ x=-1.\]
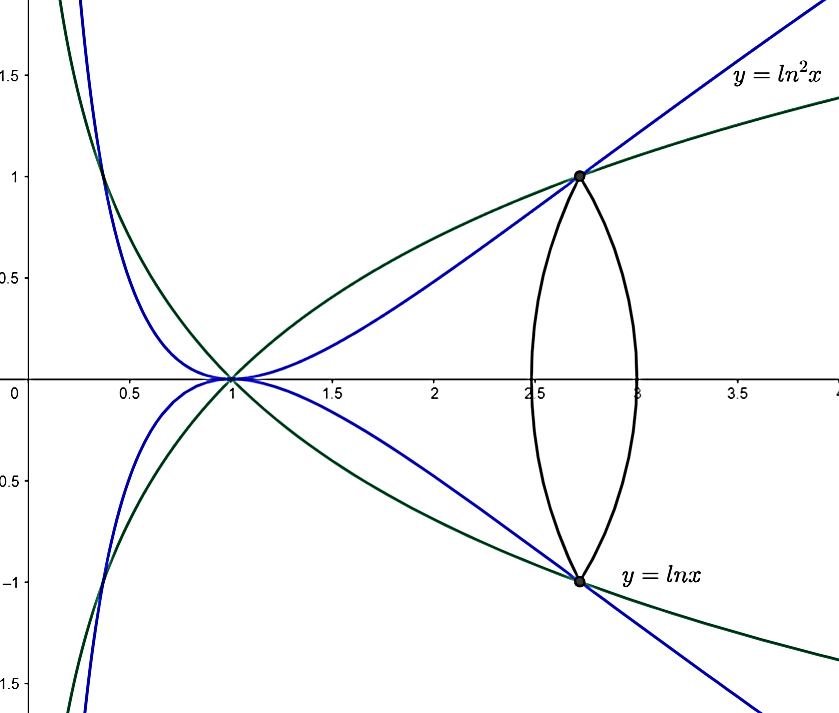
Задатак 3. Израчунати запремину тела које настаје ротацијом фигуре, ограничене кривама `y=lnx,y=ln^2x`, око `x`-осе.
Решење. Укупну запремину добијамо разликом запремина насталих тела ротацијом: \[V=V_1-V_2.\] Решавамо систем, да бисмо добили границе:
\[ \left.\ \begin{matrix}y=ln\ x\\y=ln^2x\\\end{matrix}\right\}\ \Longrightarrow\ lnx=ln^2x\ \ \Longrightarrow\ lnx\left(ln\ x-1\right)=0\Longrightarrow\ lnx=0\ \ \vee\ \ lnx=1;\ \]
Затим рачунамо појединачно запремине `V_1` и `V_2`: \[V_1=\pi∫_{-1}^eln^2xdx=\begin{Bmatrix} lnx=t\ \ \ \ \ x=1\rightarrow t=0 & \\ \frac{dx}{x}=dt\ \ \ x=e\rightarrow t=1 & \end{Bmatrix}=\int_{0}^{1}{t^2e^tdt=\left\{\begin{matrix}\ \ \ \ \ \ \ u=t^2\ \ \ \ \ \ e^tdt=dv\ \\du=2tdt\ \ \ \ \ e^t=v\ \\\end{matrix}\right\}}=\left.t^2e^t\right|_0^1-\int_{0}^{1}{2te^tdt=}π(e-2).\] \[V2=π∫_{-1}^1ln^4xdx=\pi(9e-24)\Rightarrow V=\pi\left(e-2\right)-\pi\left(9e-24\right)\ \Rightarrow V=(e-2-9e+24)-\pi(22-8e)\]