Задатак 1. Израчунати дужину лука криве `y=\frac{2}{3}x^{3/2}` од координатног почетка до тачке `(8,\frac{32\sqrt2}{3})`.
Решење. Непосредно на основу формуле добијамо:
\[l=∫_{0}^8\sqrt{1+\left(x^{1/2}\right)^2}dx=∫_{0}^8\sqrt{1+x}dx=∫_{0}^8(1+x)^\frac{1}{2}dx=\frac{(1+x)^\frac{3}{2}}{\frac{3}{2}}|_{0}^8=\frac{52}{3} \]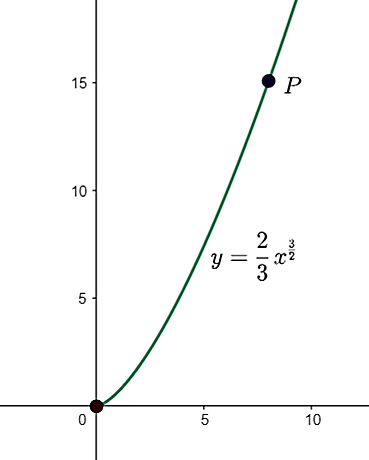
Задатак 2. Израчунати дужину лука криве `y^2=x^3` од тачке `(0,0)` до тачке `(4, 8)`.
Решење. Непосредно на основу формуле добијамо:
\[l=∫_{0}^4\sqrt{1+\frac{9x}{4}}dx=\frac{4}{9}∫_{0}^{10} t^\frac{1}{2}dt=\frac{4}{9}\frac{t^\frac{3}{2}}{\frac{3}{2}}|_{0}^{10}=\frac{8}{27}(10\sqrt10-1) \]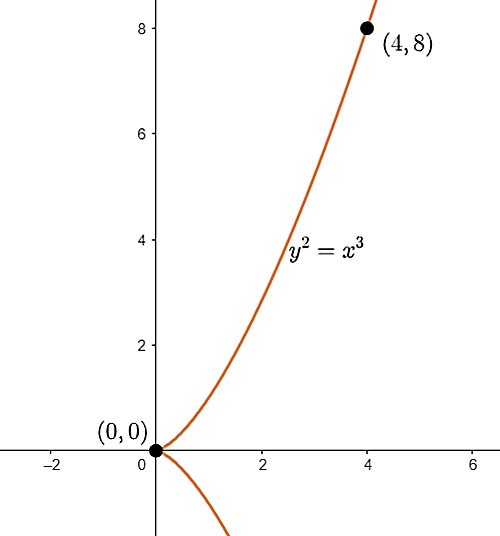
Задатак 3. Израчунај дужину лука криве `x = \frac{1}{4}y^2 - \frac{1}{2}\ln y` за `1 \leq y \leq e`.
Решење. Приметимо да је крива облика `x=f(y)`, па се зато границе одређеног интеграла посматрају по променљивој `y`.
\[l=∫_{1}^e\sqrt{1+x^{\prime2}}dy=∫_{1}^e\sqrt{1+\frac{1}{4}\left(y-\frac{1}{y}\right)^2}dx=\frac{1}{2}∫_{1}^e\left(\frac{1}{y}+y\right)dy=\frac{1}{4}\left(1+e^2\right). \]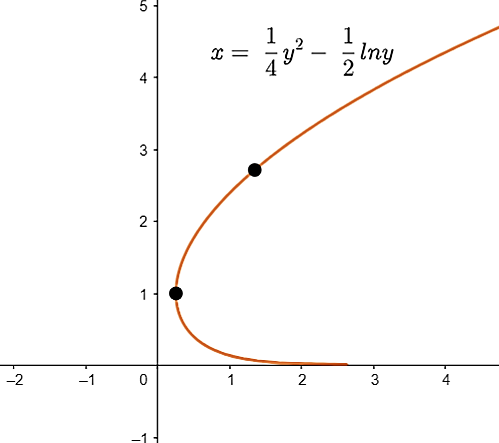
Задатак 4. Израчунати дужину лука параболе `y=\frac{x^2}{2p}` на интервалу `[0,a],a>0`.
Решење.
\[l=∫_{0}^a\sqrt{1+y^{\prime2}}dx=\frac{1}{p}∫_{0}^{a}\sqrt{x^2+p^2}dx=\frac{1}{p}(\frac{1}{2}x\sqrt{x^2+p^2}+\frac{p^2}{2}ln(x+\sqrt{x^2+p^2}))|_{0}^{a}=\frac{a}{2p}\sqrt{a^2+p^2}+\frac{p}{2}ln\frac{a+\sqrt{a^2+p^2}}{p}. \]