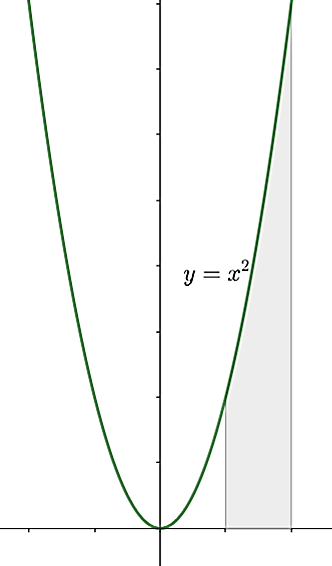
Задатак 1. Израчунати површину фигуре ограничене параболом `y = x^2`, `x`-осом и правама `x=a` и `x=b`.
Решење. Фигура о којој је реч је један криволинијски трапез. Зато је њена површина `P`, према ономе што је наведено у тексту задатка:
\[ P=∫_{a}^bx^2 dx=\frac{x^3}{3}|_{a}^b=\frac{1}{3}(b^3-a^3). \]
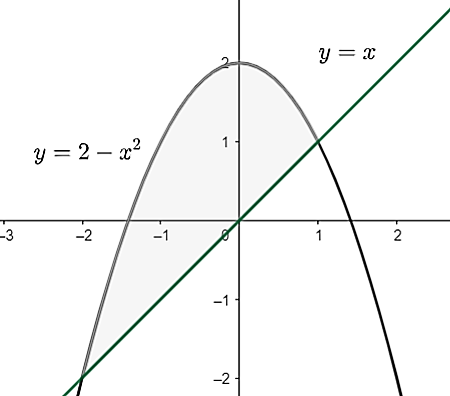
Задатак 2. Израчунати површину фигуре ограничене правом `y=x` и параболом `y=2-x^2`.
Решење. Нађимо апсцисе пресечних тачака праве и параболе решавањем система једначина:
\[y=x,\ y=2-x^2.\]
Када смо решили систем, добили смо: \[x_1=-2 \quad и\quad x_2=1.\] То ће и бити границе интеграције. Тражена површина је:
\[ P=∫_{-2}^1[(2-x^2)-x]dx=\left(2x-\frac{x^3}{3}-\frac{x^2}{2}\right)|_{-2}^1=\left(2-\frac{-2}{1}-\frac{1}{2}\right)-\left(-4+\frac{8}{3}-2\right)=\frac{9}{2}. \]
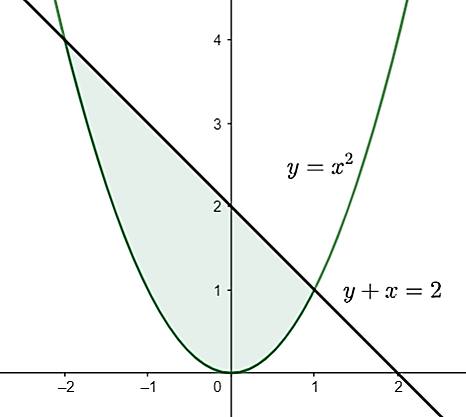
Задатак 3. Израчунати површину фигуре ограничене параболом `y=x^2` и правом `y+x=2`.
Решење. На самом почетку задатка треба одредити границе, тачније апсцисе пресечних тачака дате параболе и праве. Решавањем система \[y=x^2 \quad и\quad y=2-x\] добијамо тражене апсцисе \[x_1=1\quad и\quad x_2=-2.\] Подинтегралну функцију формирамо тако што од једначине праве одузмемо једначину параболе.
\[ P=∫_{-2}^1(2-x-x^2)dx=∫_{-2}^12dx-∫_{-2}^1xdx-∫_{-2}^1x^2dx=2x|_{-2}^1-\frac{x^2}{2}|_{-2}^1-\frac{x^3}{3}|_{-2}^1=2\left(1-\left(-2\right)\right)-\frac{1}{2}\left(1^2-\left(-2\right)^2\right)-\frac{1}{3}\left(1^3-\left(-2\right)^3\right)=\frac{9}{2}. \]
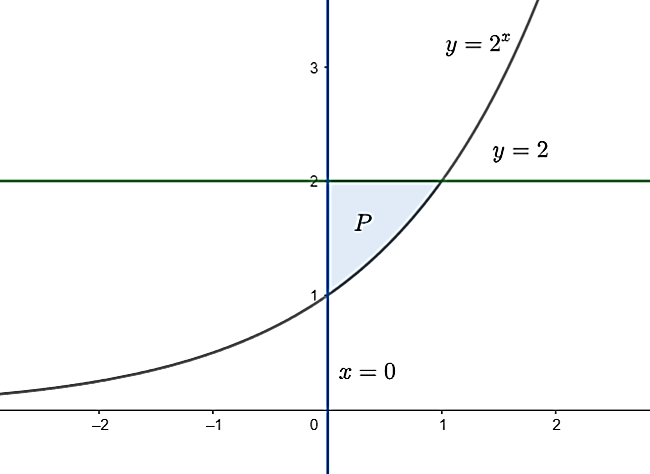
Задатак 4. Израчунати површину фигуре ограничене кривом `y=2^x` и правама `y=2` и `x=0` .
Решење. Границе настале фигуре ћемо одредити решавањем два система. Решавање система \[y=2^x\quad и\quad y=2\] нам даје апсцису `x=1`, друга апсциса је `x=0`. Тражена површина се добија разликом једначине праве `y=2` и једначином експоненцијалне функције `y=2^x`.
\[ P=∫_{0}^1(2-2^x)dx=∫_{0}^12dx-∫_{0}^12^xdx=2x|_{0}^1-\frac{2^x}{ln2}|_{0}^1=2-\frac{1}{ln2} \]
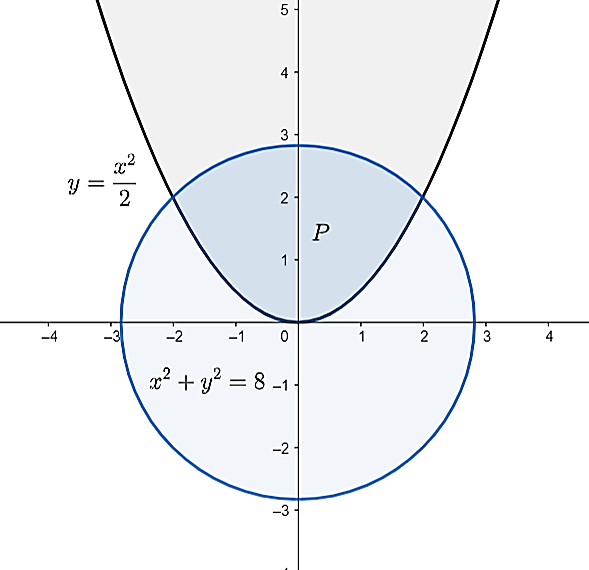
Задатак 5. Израчунати површину фигуре ограничене кривама `y = \frac{x^2}{2}` и `x^2+y^2=8`.
Решење. Да бисмо одредили границе настале фигуре решавамо систем и добијамо да су решења `x=2` и `x=-2`.
\[y^2=8-x^2, y=\pm\sqrt{8-x^2};\]
\[P=∫_{-2}^2(\sqrt{8-x^2}-\frac{x^2}{2})dx=2∫_{0}^2\sqrt{8-x^2}dx-∫_{0}^2\frac{x^2}{2}dx=2\pi+\frac{4}{3}.\]
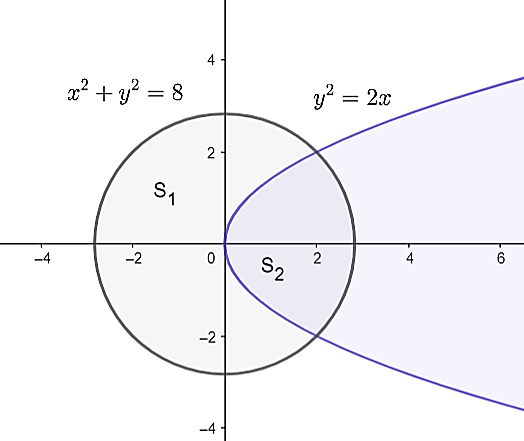
Задатак 6. У ком односу парабола `y^2=2x` дели површину круга `x^2+y^2=8`?
Решење. Нека је `S_1` површина круга, а `S_2` површина коју чине параболички и кружни сегмент. Очигледно, `S_1=8\pi`. Решавањем система једначина: \[y^2= 2x \quad и\quad x^2+y^2=8\] добијамо апсцису `x=2` пресечне тачке параболе и круга. Сада је:
\[ S_2=2\left(2\pi-\int_{0}^{2}\left(\sqrt{8-x^2}-\sqrt{2x}\right)dx\right)=2\left(2\pi-\int_{0}^{2}\sqrt{8-x^2}+\left.\ \frac{2}{3}\sqrt2x^\frac{3}{2}\right|_0^2\right)=2\left(2\pi+\frac{8}{3}-4\int_{0}^{\frac{\pi}{4}}\left(1+cos2t\right)dt\right)=2\pi+\frac{4}{3}. \]
\[\left(S_1-S_2\right):S_2=\left(8\pi-2\pi-\frac{4}{3}\right):S_2=\left(9\pi-2\right):\left(3\pi+2\right).\]