Задатак 1. Наћи дужину лука криве задату параметарски \[x=a\left(t-sin\ t\right);y=a\left(1-\cos{t}\right), 0\le t\le2\pi.\]
Решење. Примењујемо формулу за дужину лика криве задате параметирски, самим тим рачунамо \[x^\prime\left(t\right)=atcost;y^\prime\left(t\right)=atsint; x^{\prime2}\left(t\right)+y^{\prime2}\left(t\right)=a^2t^2:\]
\[L=a\int_{0}^{2\pi}tdt=\left.\ \frac{at^2}{2}\right|_0^{2\pi}=2\pi^2a.\]
Задатак 2. Наћи површину фигуре ограничене кривама које су дате параметарски \[x=2t-t^2,\ \ y=2t^2-t^3.\]
Решење. Крива сама себе сече у координатном почетку: `x=0` за `t=0` i `t=2; y=0` такође за `t=0` и `t=2`. За израчунавање површине користићемо формулу:
\[\begin{matrix}S&=\frac{1}{2}\int_{0}^{2}\left(x\left(t\right)y^\prime\left(t\right)-y\left(t\right)x^\prime\left(t\right)\right)dt=\frac{1}{2}\int_{0}^{2}\left(t^4-4t^3+4t^2\right)dt=\left.\ \frac{1}{2}\left(\frac{t^5}{5}-t^4+\frac{4}{3}t^3\right)\right|_0^2=4\left(\frac{4}{3}-2+\frac{4}{5}\right)=\frac{8}{15}.\\&\\\end{matrix}\].
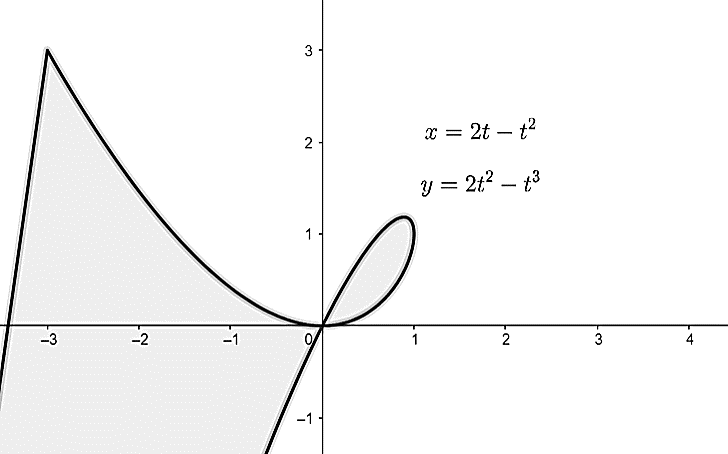
Задатак 3. Наћи површину фигуре ограничене кривама које су дате параметарски \[x=a\left(2cos\ t-\cos{2t}\right);y=a\left(2sin\ t-\sin{2t}\right).\]
Решење. Фигура је ограничена и затворена \[\left(x\left(0\right)=x\left(2\pi\right);y\left(0\right)=y\left(2\pi\right)\right),\] следи:
\[S=\frac{1}{2}\int_{0}^{2\pi}\left(x\left(t\right)y^\prime\left(t\right)-x^\prime\left(t\right)y\left(t\right)\right)dt=a^2\int_{0}^{2\pi}\left(3-3cos t\right)dt=6\pi a^2.\]
Задатак 4. Наћи дужину лука криве задату параметарски \[x=a\left(t-sin\ t\right);y=a\left(1-\cos{t}\right), 0\le t\le2\pi.\]
Решење. Примењујемо формулу за дужину лика криве задате параметирски , самим тим рачунамо \[x^\prime\left(t\right)=a\left(1-cos\ t\right),\ \mathcal{V}^\prime\left(t\right)=asint;\ x^{\prime2}\left(t\right)+y^2\left(t\right)=2a^2\left(1-cos\ t\right)=4a^2\sin^2\frac{t}{2} :\]
\[L=2a\int_{0}^{2\pi}sin\frac{t}{2}dt=4a\int_{0}^{a}sin\ zdz=\left.\ 4acos\ z\right|_0^\pi=8a.\]
Задатак 5. Наћи површину повши која се добија ротацијом `x^\frac{2}{3}+y^\frac{2}{3}=a^\frac{2}{3}` око осе `Ox`.
Решење. Параметарске једначине астроиде имају облик \[x=a\cos^3t;y=a\sin^3t; \left(0\le t\le2\pi\right),\] тада је \[dl=3a\left|sin\ tcos\ t\right|dt.\] Узимајући у обзир симетричност криве у односу на обе координатне осе, имамо:
\[\begin{matrix}P&=4\pi\int_{0}^{\frac{\pi}{2}}y\left(t\right)dl\left(t\right)=12\pi a^2\int_{0}^{\frac{\pi}{2}}\sin^4td\left(sin\ t\right)=\left.\ \frac{12}{5}\pi a^2\sin^5t\right|_0^{\frac{\pi}{2}}=\frac{12}{5}\pi a^2\\&\\\end{matrix}.\]