Algebarske krive ili nama najzanimljivije ravne algebarske krive su one krive koje se mogu predstaviti jednačinom i to takvom da je ona zapravo polinom (to su takozvane polinomijalne jednačine).

Kako to krivu možemo predstaviti polinomom i zašto smo istakli baš ravne algebarske krive?

Odgovor na drugo pitanje leži u tome da nas ovde interesuju samo one krive koje su sastavljene od odabranih tačaka jedne ravni, dok nam odgovor na prvo pitanje kaže da je algebarska kriva sastavljena od onih tačaka ravni čije koordinate mogu da se "ubace" u polinomijalnu jednačinu, a da je pritom zadovoljavaju.

Evo primera:



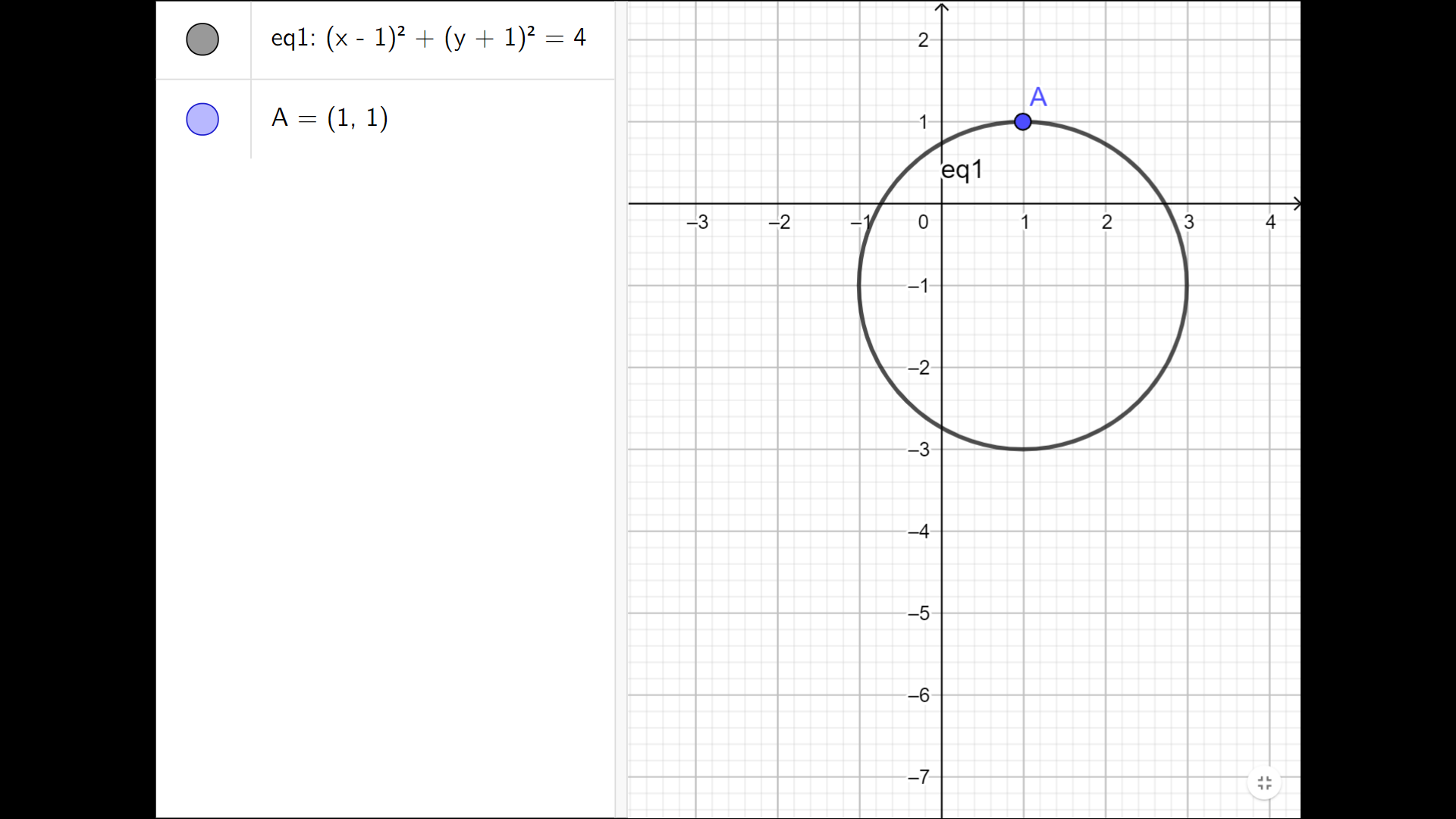
Jednačina sa slike $eq1$ jeste polinomijalna jednačina po $x$ i $y$ i ona određuje algebarsku krivu, a može se ustanoviti da je ta kriva krug. Ukoliko uzmemo proizvoljnu tačku, npr. tačku $(1,1)$ ako ona pripada našoj algebarskoj krivoj ona mora zadovoljavati polinomijalnu jednačinu kojom je ta kriva zadata. Zaista: $1^2+1^2-2\cdot1+2\cdot1+2=4$ što nam govori da tačka $(1,1)$ pripada našoj algebarskoj krivoj zadatom jednačinom $eq1$, dok za neku drugu tačku to možda ne bi bio slučaj.

Znajući sada sve ovo, hajde da uvedemo i zvaničnu definiciju realne algebarske krive. Umesto ravne, ovaj put naglašavamo da je algebarska kriva realna, jer ćemo za ravan uzeti baš realnu ravan ${\mathbb{R}}^2$.

Definicija. Realna algebarska kriva $C$ je podskup od ${\mathbb{R}}^2$ i ona čini geometrijsko mesto tačaka nula polinoma $P(x,y)$ sa realnim koeficijentima, zapisano matematičkom notacijom: $$C=\{(x,y)\in{\mathbb{R}}^2\mid P(x,y)=0\}$$

Za kraj ovog poglavlja spomenimo i oblasta matematike u kojoj se ove krive proučavaju.
Algebarska geometrija je oblast matematike koja se bavi ovakvim krivama, preciznije ona se bavi svim algebarskim varijetetima. (npr. pored algebarskih krivih koje su dimenzije jedan, takođe su i algebarske površi primer algebarskih varijeteta, a one su dimenzije dva), no nas u ovom radu zanimaju samo algebarske krive.