Стефан Малбашић,
Универзитет у Београду, Математички факултет

Дворазмјера. Хармонијска спрегнутост. Перспективитет. Пројективитет.

Дворазмјера.

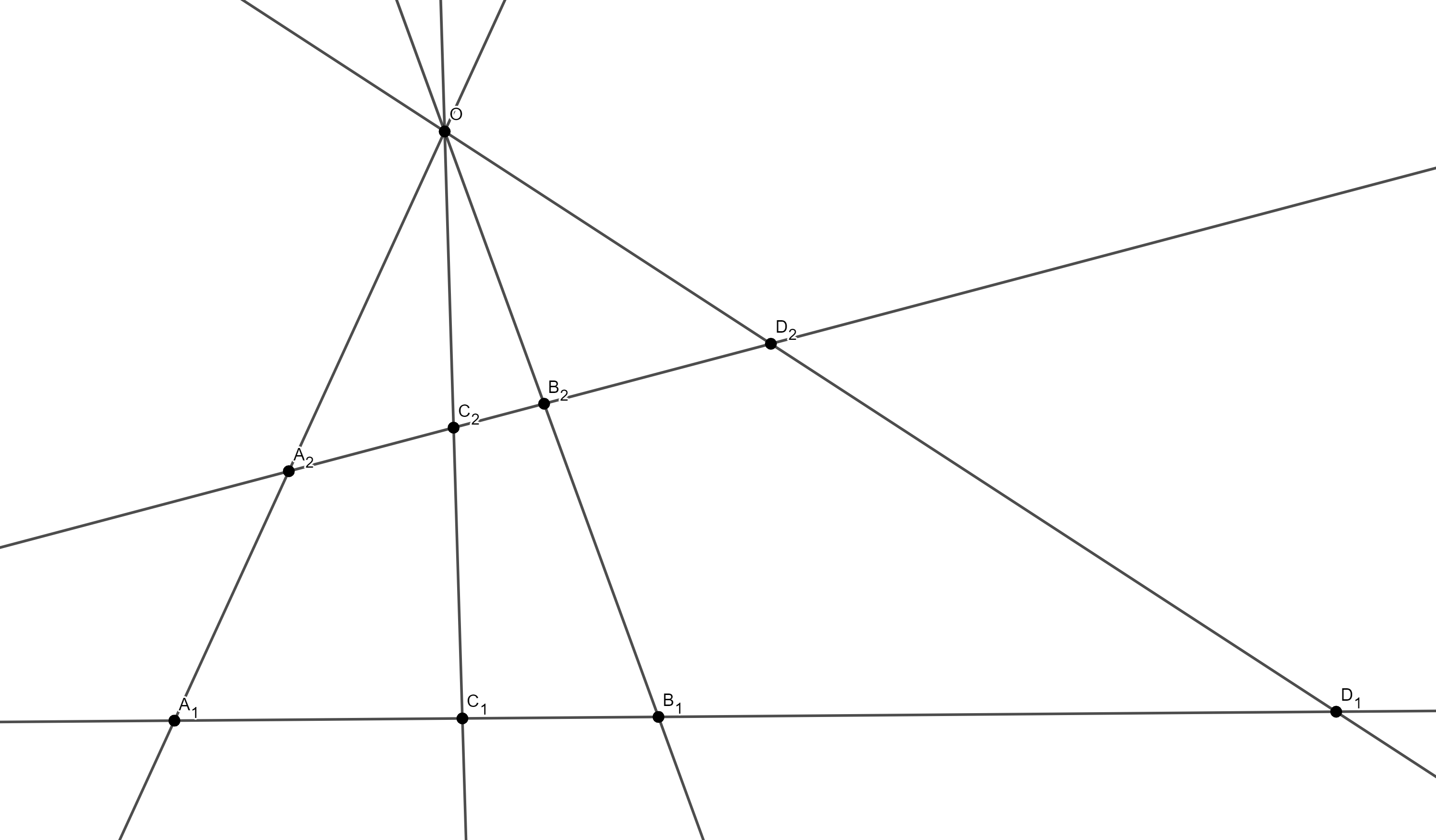
Дефиниција. Нека су тачке $A$, $B$, $C$ и $D$ колинеарне. Дворазмјера парова тачака $A$, $B$, $C$ и $D$ је: $$R(A,B;C,D) = \frac{\overrightarrow{AC}}{\overrightarrow{CB}}:\frac{\overrightarrow{AD}}{\overrightarrow{DB}}$$ Нека су $a$, $b$, $c$, $d$ четири праве које припадају једном прамену. За дате праве $p_1$ и $p_2$ означимо $A_i = a \cap p_i$, $B_i = b \cap p_i$, $C_i = c \cap p_i$, $D_i = d \cap p_i$, за $i = 1, 2$. Тада је $$R(A_1,B_1;C_1,D_1) = R(A_2,B_2;C_2,D_2).$$ Зато је коректно дефинисати дворазмјеру парова правих једног прамена као $$R(a,b;c,d)=R(A_1,B_1;C_1,D_1).$$
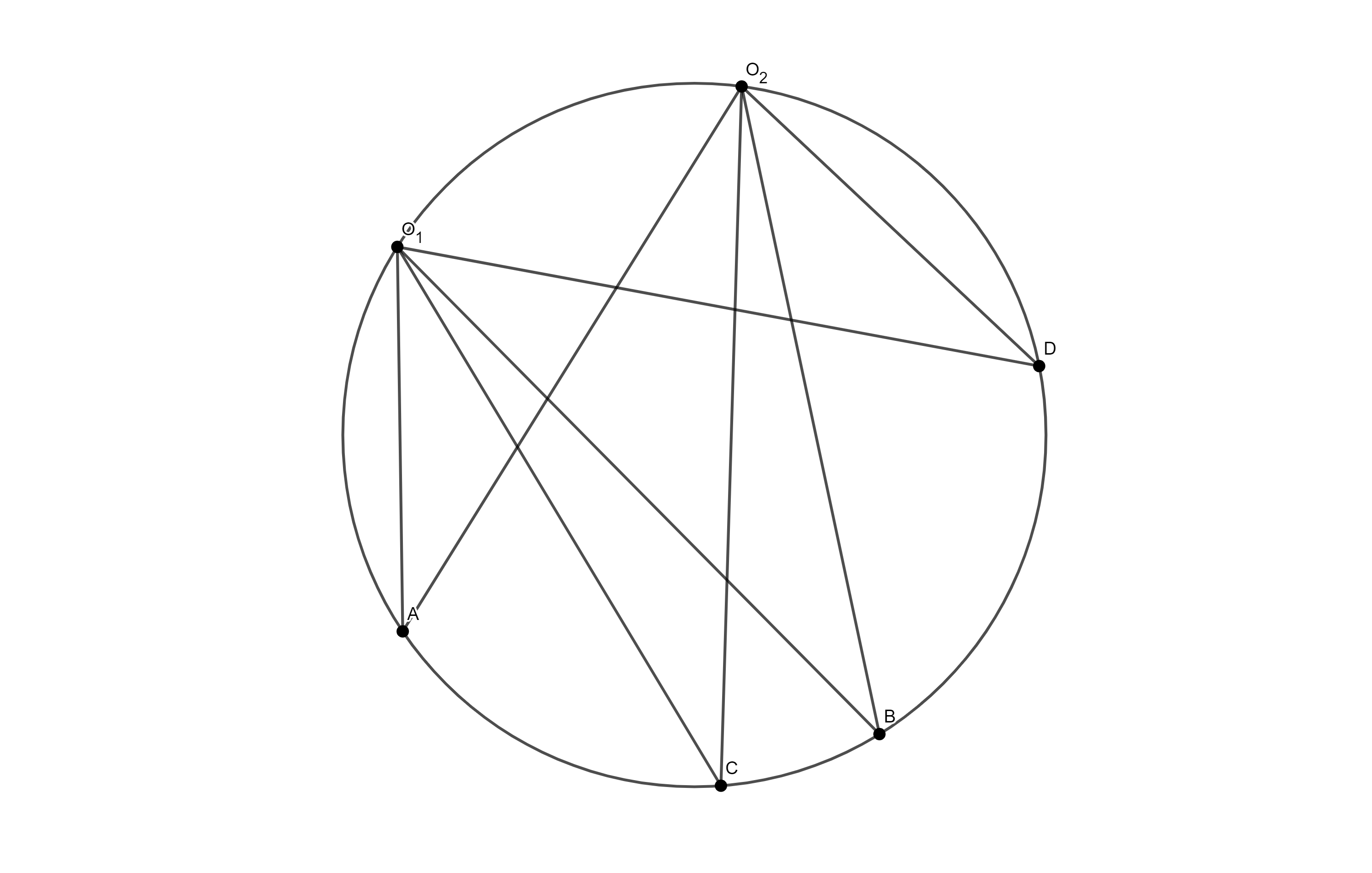
Нека су $O_1$, $O_2$, $A$, $B$, $C$, $D$ коцикличне тачке. Тада је $$R(O_1A,O_1B;O_1C,O_1D) = R(O_2A,O_2B;O_2C,O_2D)$$ Зато је коректно дефинисати дворазмјеру парова тачака за коцикличне тачке, као $$R(A,B;C,D)=R(O_1A,O_1B;O_1C,O_1D).$$
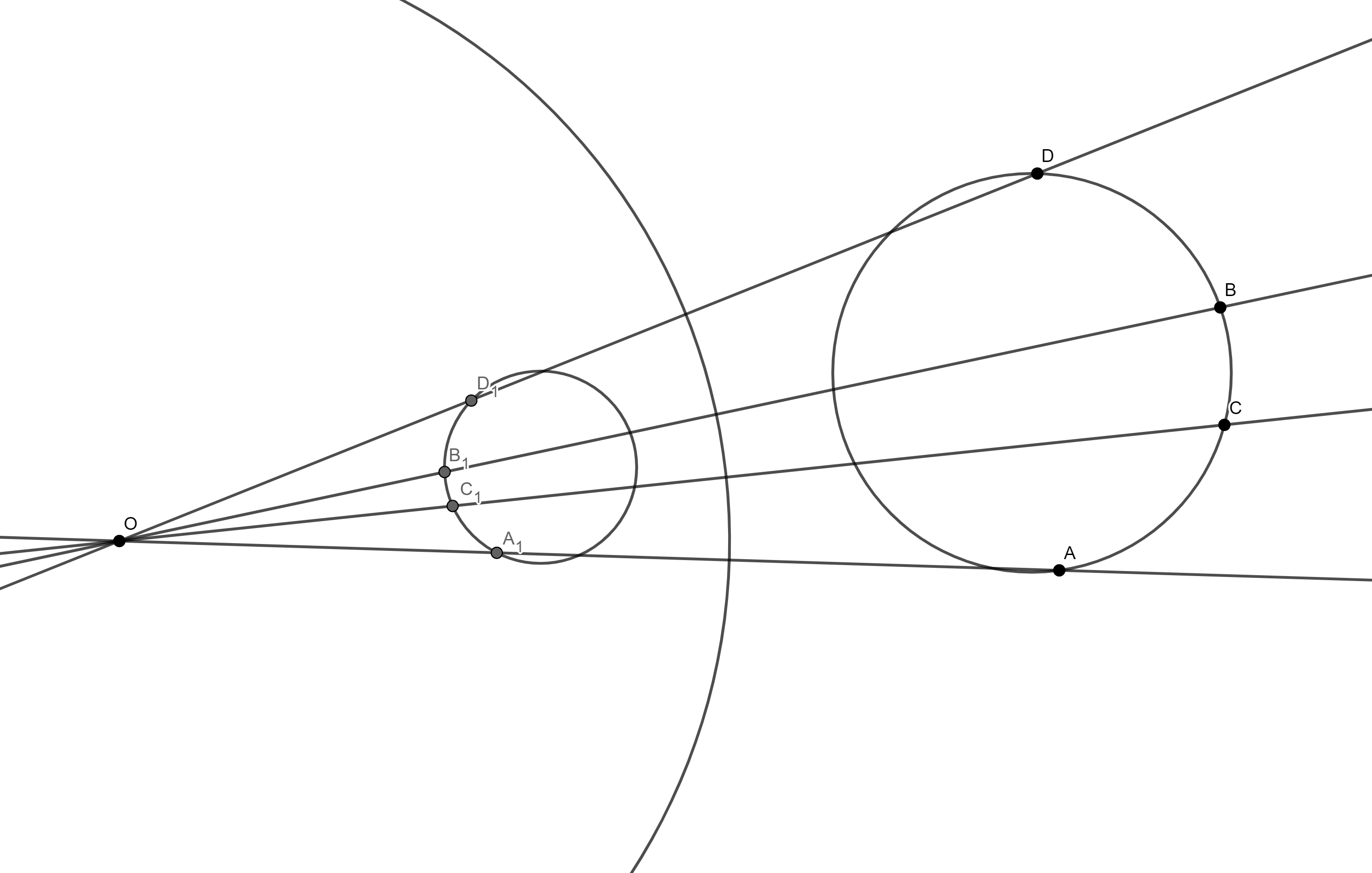
Нека су $A$, $B$, $C$ и $D$ колинеарне или коцикличне тачке, и нека инверзија са центром у $O$ пресликава тачке $A$, $B$, $C$, $D$ у тачке $A^*$, $B^*$, $C^*$, $D^*$. Тада је $$R(A,B;C,D) = R(A^*,B^*;C^*,D^*).$$

Хармонијска спрегнутост.

Дефиниција. Нека су тачке $A$, $B$, $C$ и $D$ колинеарне или коцикличне. Парови тачака $A$, $B$ и $C$, $D$ су хармонијски спрегнути ако је $R(A, B; C, D) = −1$, што се означава и са $H(A, B; C, D)$.

Перспективитет. Пројективитет.

Дефиниција. Перспективитет у односу на тачку $S$, у ознаци $\stackrel{S}{=}$, je свако пресликавање праве или круга $l_1$ на праву или круг $l_2$, такво да уколико je $l_1$ или $l_2$ круг онда садржи и тачку $S$, при коме се свака тачка $A_1 \in l_1$ слика у тачку $A_2 = OA_1 \cap l_2$. Према претходним ставовима, перспективитет чува дворазмјеру, a самим тим и хармонијску спрегнутост.

Дефиниција. Пројективитет je свако пресликавање праве или круга $l_1$ на праву или круг $l_2$ које се може представити као композиција перспективитета.

Теорема 1. Нека су тачке $A$, $B$, $C$, $D_1$ и $D_2$ колинеарне или концикличне. Ако je $R(A,B; C,D_1) = R(A,B; C,D_2)$, онда je $D_1=D_2$. Другим ријечима, пројективитет са три фиксне тачке је идентитет.

Теорема 2. Ако су тачке $A$, $B$, $C$, $D$ међусобно различите и $R(A, B; C, D) = R(B, A; C, D)$ онда je $H(A, B; C, D)$.