Стефан Малбашић,
Универзитет у Београду, Математички факултет

Бријаншонова и Брокарова теорема.

Бријаншонова теорема: У тангентном шестоуглу $A_1A_2A_3A_4A_5A_6$ дијагонале $A_1A_4$, $A_2A_5$ и $A_3A_6$ се сијеку у једној тачки.

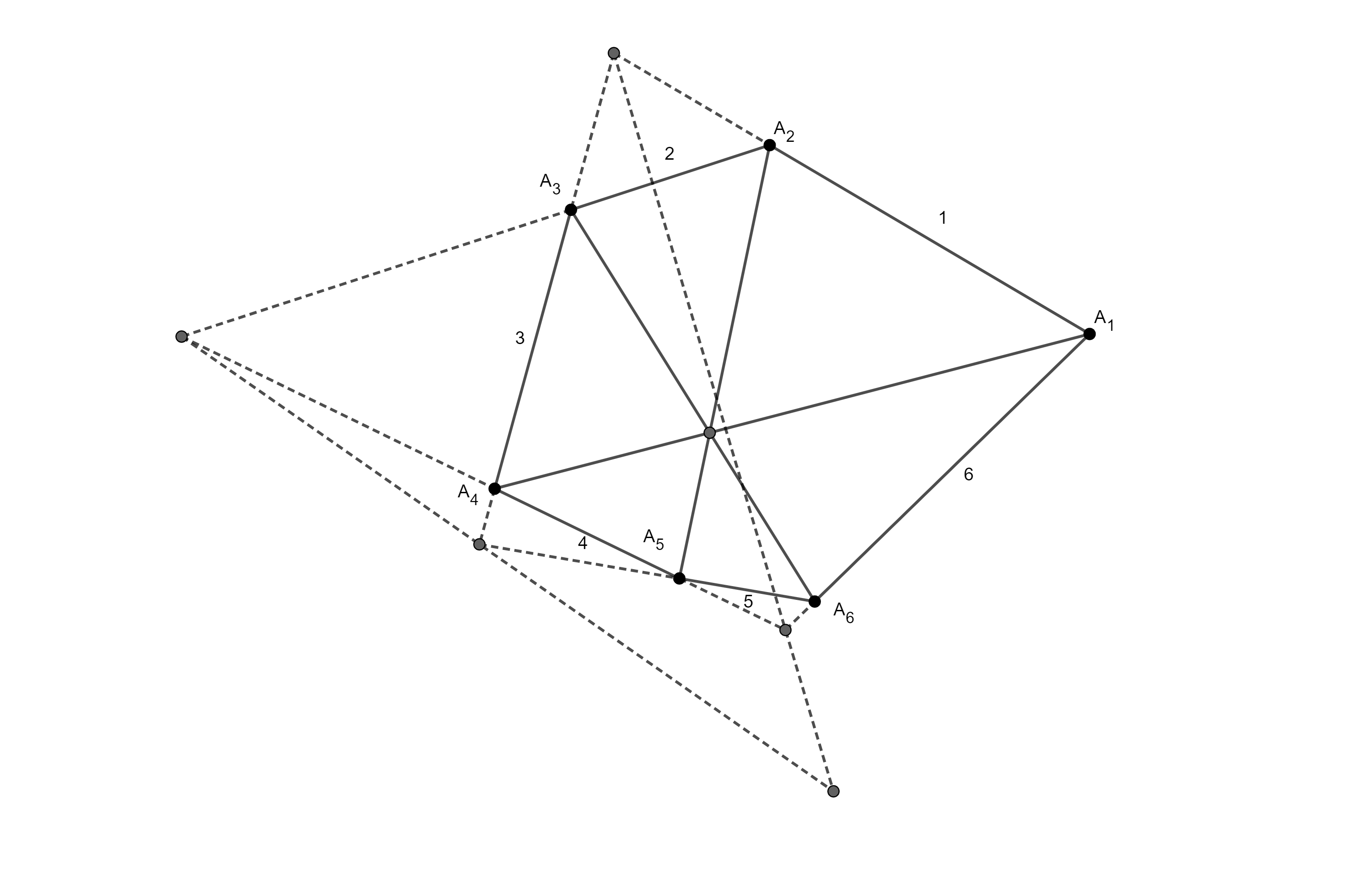
Доказ: Користићемо конвенцију по којој тачку и праву који су у односу пол-полара означавамо истим малим и великим словом абецеде. Означимо са $M_i$, $i = 1, 2, . . ., 6$, тачку додира стране $A_iA_{i+1}$ са кругом $k$. Како je $m_i = A_iA_{i+1}$, важи и $M_i \in a_i$, $M_i \in a_{i+1}$, пa je $a_i = M_{i−1}M_i$.
Нека je $b_j = A_jA_{j+3}$, $j = 1, 2, 3$. Тада je $B_j = a_j \cap a_{j+3} = M_{j−1}M_j \cap M_{j+3}M_{j+4}$. Треба доказати да постоји тачка $P$ таква да $P \in b_1, b_2, b_3$, или аналогно, да постоји права $p$ таква да $B_1, B_2, B_3 \in p$. Другим ријечима, треба доказати да су $B_1$, $B_2$, $B_3$ колинеарне. Међутим, то слиједи непосредно из Паскалове теореме, ако je примијенимо на тетивни шестоугао $M_1M_3M_5M_4M_6M_2$. $\square$

Резимирајући управо изложени доказ, можемо рећи да се Бријаншонова теорема добија из Паскалове теореме замјеном свих тачака њиховим поларама и свих правих њиховим половима.

Бријаншонова и Паскалова теорема су дуалне, јер се једна из друге добијају поларним пресликавањем. И овдје можемо посматрати дегенерисани случај када су нека од тјемена шестоугла на кругу.

Примјер. Нека су $D$, $E$, $F$ додирне тачке уписаног круга $\Delta ABC$ са страницама $BC$, $CA$, $AB$ редом. Бријаншонова теорема на дегенерисаном шестоуглу $AFBDCE$ нам даје да се $AD$, $BE$ и $CF$ сијеку у једној тачки (тзв. Жергоновој тачки).

Посљедица. Ако уписани круг тангентног четвороугла $ABCD$ додирује странице $AB$, $BC$, $CD$, $DA$ редом у тачкама $M$, $N$, $P$, $Q$, онда се праве $AC$, $BD$, $MP$ и $NQ$ сијеку у једној тачки.

Доказ: Примјеном Бријаншонове теореме на дегенерисани шестоугао $AMBCPD$ добијамо да $MP$ пролази кроз пресјек дијагонала $AC$ и $BD$. Аналогно, и $NQ$ пролази кроз ту тачку. $\square$

Посматрајмо сада тангентни четвороугао $ABCD$ и његов уписани круг $k$, и означимо са $E$, $F$, $G$ пресјеке правих $AB$ са $CD$, $BC$ са $DA$, и $AC$ са $BD$, редом. Нека $k$ додирује странице $AB$, $BC$, $CD$ и $DA$ редом у тачкама $M$, $N$, $P$ и $Q$. По Бријаншоновој теореми, тачка $G$ je на правој $MP$. Како je $MP$ полара тачке $E$ (у односу на $k$), то тачка $E$ лежи на полари тачке $G$. Аналогно и $F$ лежи на тој полари. Према томе:

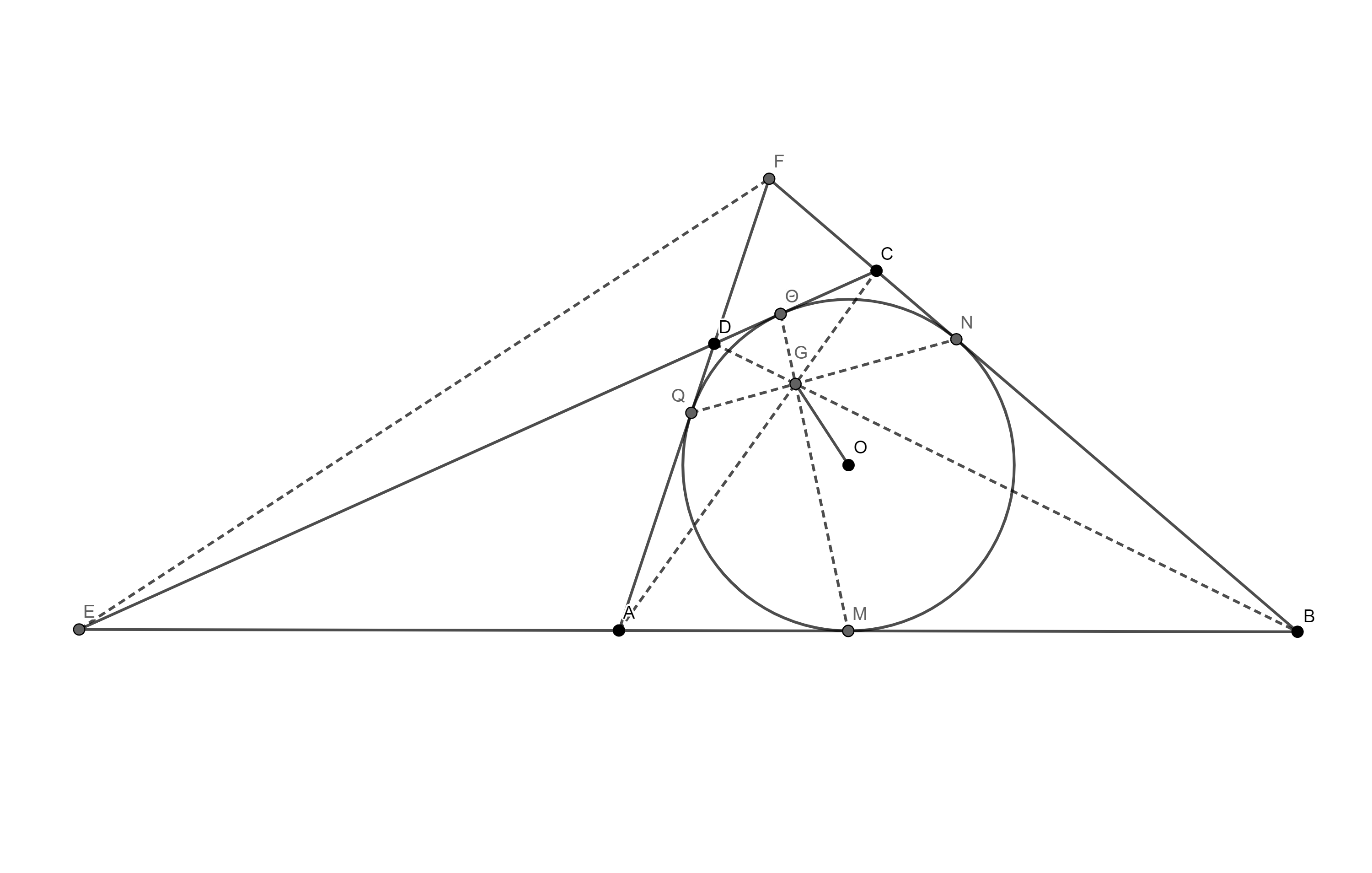
Теорема 7. Нека je $ABCD$ четвороугао описан око круга $k$ са центром $O$. Ако се праве $AB$ и $CD$ сијеку у $E$, $BC$ и $DA$ у $F$, a $AC$ и $BD$ у $G$, онда je $EF$ полара тачке $G$. Одавде je $OG \bot EF$.

Овде не можемо по аналогији да закључимо да je и $OE \bot FG$ (нити je то тачно), јер je редослијед тачака $A$, $B$, $C$, $D$ битан: $ABCD$ je тангентан четвороугао, али $ACBD$ то није.

Посљедица. У тангентном трапезу $ABCD$ ($AB||CD$) који није ромб, права $OG$ je нормална на $AB$, гдје je $O$ центар уписаног круга и $G$ пресјек дијагонала.

Доказ: Слиједи из T.7 у дегенерисаном случају. Овдје je тачка $E = AB \cap CD$ бесконачна, па je $EF||AB$. $\square$

Брокарова теорема: Дат je тетивни четвороугао $ABCD$, уписан у круг $k$ са средиштем $O$. Нека je $E = AB \cap CD$, $F = AD \cap BC$, $G = AC \cap BD$. Тада je $O$ ортоцентар троугла $EFG$.

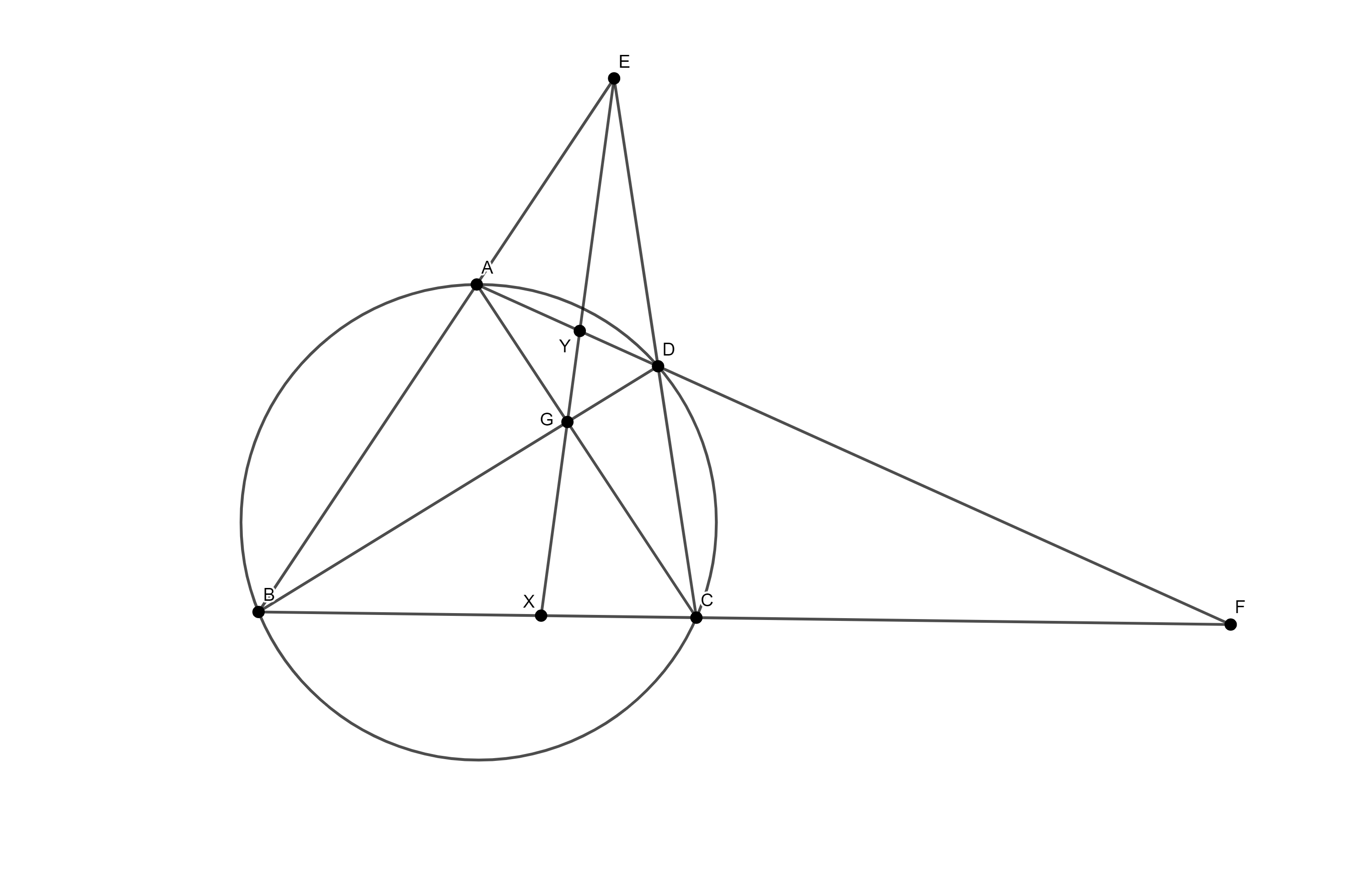
Доказ: Доказаћемо да je права $EG$ полара тачке $F$. Означимо $X = EG \cap BC$ и $Y = EG \cap AD$. Тада je $$ADYF \stackrel{E}{=}BCXF \stackrel{G}{=}DAYF,$$ одакле добијамо $H(A, D; Y, F)$ и $H(B, C; X, F)$. Према једној од карактеризација поларе наведених раније у тексту (Теорема 5), тачке $X$ и $Y$ леже на полари тачке $F$, одакле слиједи да je права $EG$ полара тачке $F$. Како je $EG$ полара тачке $F$, важи $EG \bot OF$. Аналогно je и $FG \bot OE$, па je $O$ ортоцентар троугла $EFG$. $\square$