Стефан Малбашић,
Универзитет у Београду, Математички факултет

Задаци.

Задатак 1: (теорема o лептиру) На кругу $k$ се налазе тачке $M$ и $N$. Ако je $P$ средиште тетиве $MN$, a $AB$ и $CD$ ($A$ и $C$ су са исте стране $MN$) произвољне двије тетиве круга $k$ које садрже тачку $P$, тада дужи $AD$ и $BC$ тетиву $MN$ сијеку у тачкама које се налазе на једнаким растојањима од $P$.

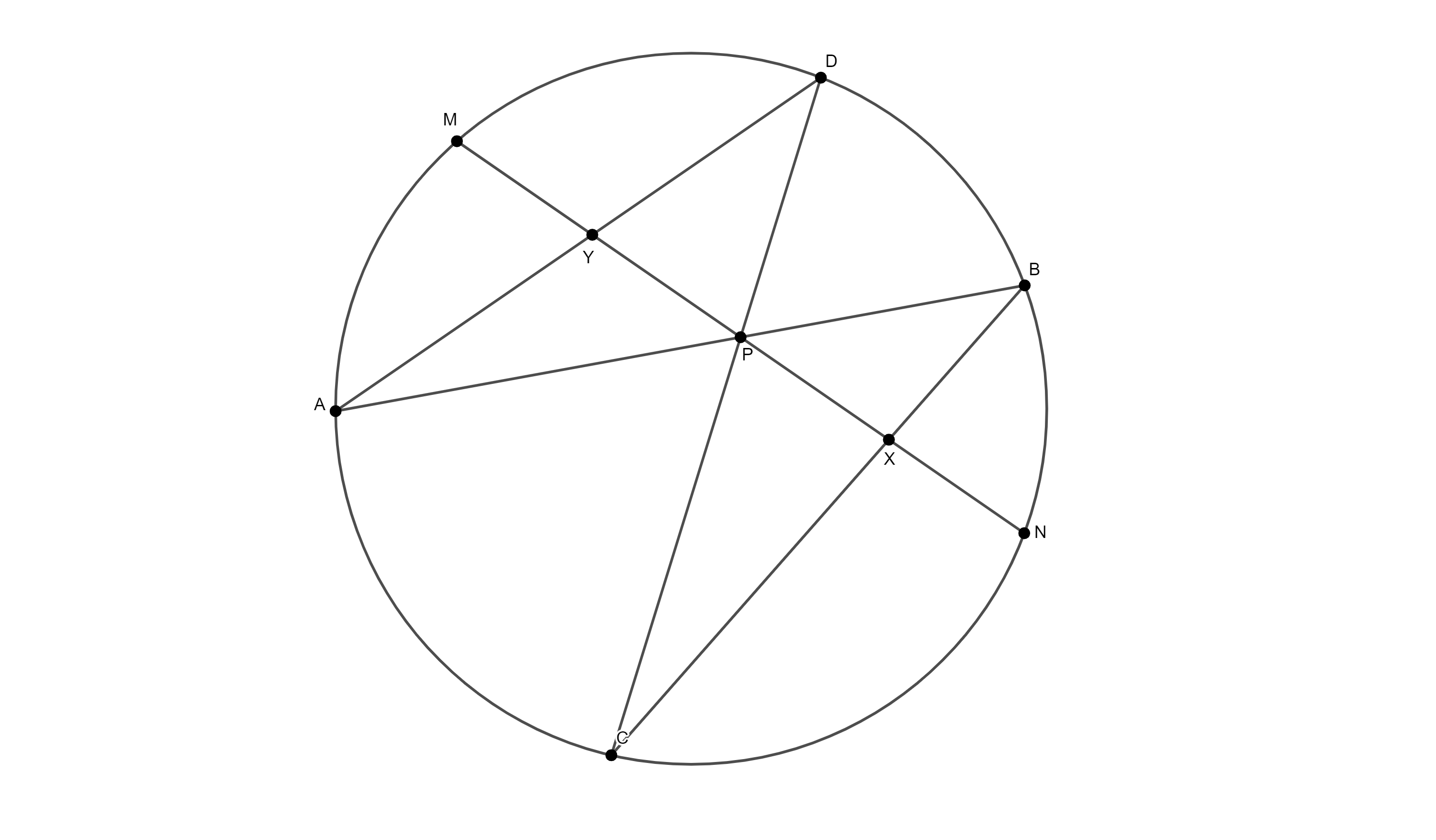
Рјешење: Нека је $AD \cap MN = Y$ и нека је $BC \cap MN = X$. Означимо са $X_0$ тачкуа симетричну тачки $Y$ у односу на $P$. Уочимо да je $$\begin{equation*} \begin{aligned} R(M,N;X,P) &= R(M, N; P, Y) \quad (MNXP \stackrel{D}{=} MNAC \stackrel{B}{=} MNPY) \\ &= R(N,M; P, X_0) \quad (\text{јер централна симетрија са центром у $P$,} \\ & \qquad \text{као и све изометрије, чува размјеру, a самим тим и дворазмјеру})\\ &= \frac{1}{R(N,M; X_0, P)} = R(M,N;X_0,P) \quad (\text{из општих својстава дворазмјере}) \end{aligned} \end{equation*} $$ Слиједи да je $X=X_0$.

Задатак 2: Тачка изогонално спрегнута тежишту назива се Лемуанова тачка. Праве које спајају тјемена троугла са Лемуановом тачком називају се симедијане. Нека се тангенте на описани круг $Γ$ троугла $ABC$ у тачкама $B$ и $C$ сијеку у тачки $P$. Доказати да je права $AP$ симедијана троугла $ABC$.

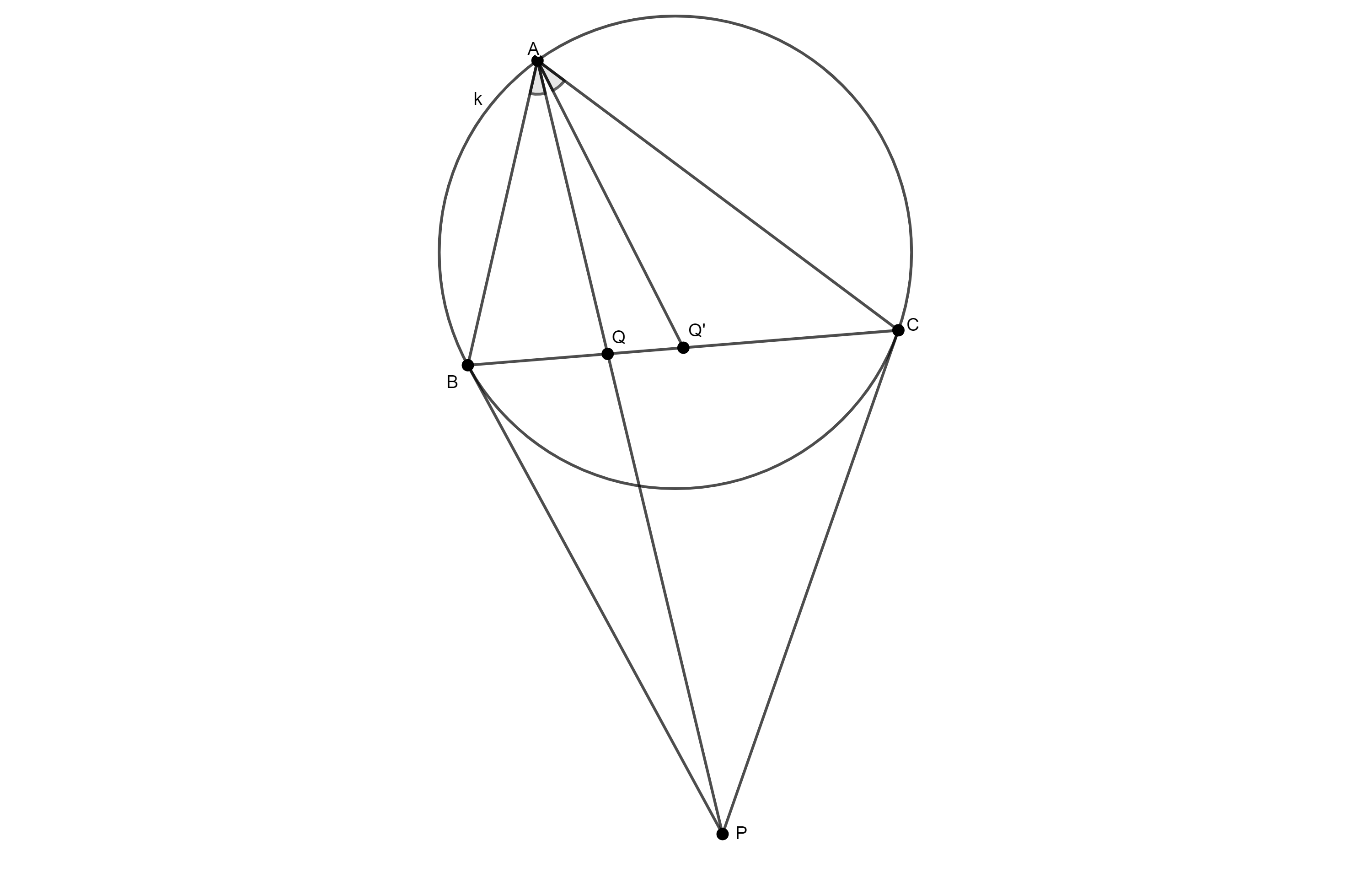
Рјешење: Означимо са $Q$ пресјек правих $AP$ и $BC$ и са $Q’$ тачку праве $BC$ такву да je полуправа $AQ’$ изогонално спрегнута полуправој $AQ$ у троуглу $ABC$. Према дефиницији изогонално спрегнутих полуправих, $\angle Q’AC = \angle BAQ$ и $\angle BAQ’ = \angle QAC$. За произвољну тачку $X$ на дужи $BC$, примјеном синусне теореме на троуглове $BAX$ и $XAC$ добијамо: $$\begin{equation*} \begin{aligned} \frac{BX}{XC} &= \frac{BX}{AX}\cdot \frac{AX}{XC} = \frac{\sin\angle BAX}{\sin\angle ABX}\cdot \frac{\sin\angle ACX}{\sin\angle XAC} \\ &= \frac{\sin\angle ACX}{\sin\angle ABX}\cdot \frac{\sin\angle BAX}{\sin\angle XAC} = \frac{AB}{AC}\cdot \frac{\sin\angle BAX}{\sin\angle XAC}. \end{aligned} \end{equation*} $$ Примјеном ове формуле на тачке $X=Q$ и $X=Q’$ и множењем добијамо $$\frac{BQ}{QC} \cdot \frac{BQ'}{Q'C} = \frac{AB}{AC}\cdot \frac{\sin\angle BAQ}{\sin\angle QAC}\cdot\frac{AB}{AC}\cdot \frac{\sin\angle BAQ'}{\sin\angle Q'AC} = \frac{AB^2}{AC^2}.$$ Дакле, уколико докажемо да је $\frac{BQ}{QC} = \frac{AB^2}{AC^2}$, одатле ће слиједити да је $\frac{BQ'}{Q'C} = 1$, односно да је $Q’$ средиште $BC$ а полуправа $AQ$ изогонално спрегнута тежишној линији, чиме ће тврђење задатка бити доказано. Како тачка $P$ припада поларама тачака $B$ и $C$, то тачке $B$ и $C$ припадају полари тачке $P$, па закључујемо да је полара тачке $P$ управо права $BC$. Уочимо тачку $D$ која се добија у пресјеку праве $BC$ са тангентом на описани круг у тачки $A$. Како тачка $D$ по дефиницији припада поларама тачака $A$ и $P$, то је полара тачке $D$ права $AP$. Одатле слиједи $H(B, C; D, Q)$.

Одредимо сада однос $\frac{BD}{DC}$: како су троуглови $ABD$ и $CAD$ слични, важи $\frac{BD}{AD} = \frac{AD}{CD} = \frac{AB}{AC}$. Одатле је $\frac{BD}{CD} = \frac{BD}{AD}\frac{AD}{CD} = \frac{AB^2}{AC^2}$. Због хармонијске спрегнутости $H(B, C; D, Q)$ важи и $\frac{BQ}{QC} = \frac{BD}{DC}=\frac{AB^2}{AC^2}$, чиме је доказано тврђење задатка.

Задатак 3: Нека je $ABC$ троугао, и $D$, $E$ тачке на страницама $AB$ и $AC$ редом тако да je $DE$ паралелно са $BC$. Нека je $P$ тачка унутар троугла $ADE$, и праве $BP$ и $CP$ сијеку $DE$ у тачкама $F$ и $G$, редом. Кругови описани око троуглова $PDG$ и $PFE$ сијеку су у тачкама $P$ и $Q$. Доказати да су тачке $A$, $P$ и $Q$ колинеарне.

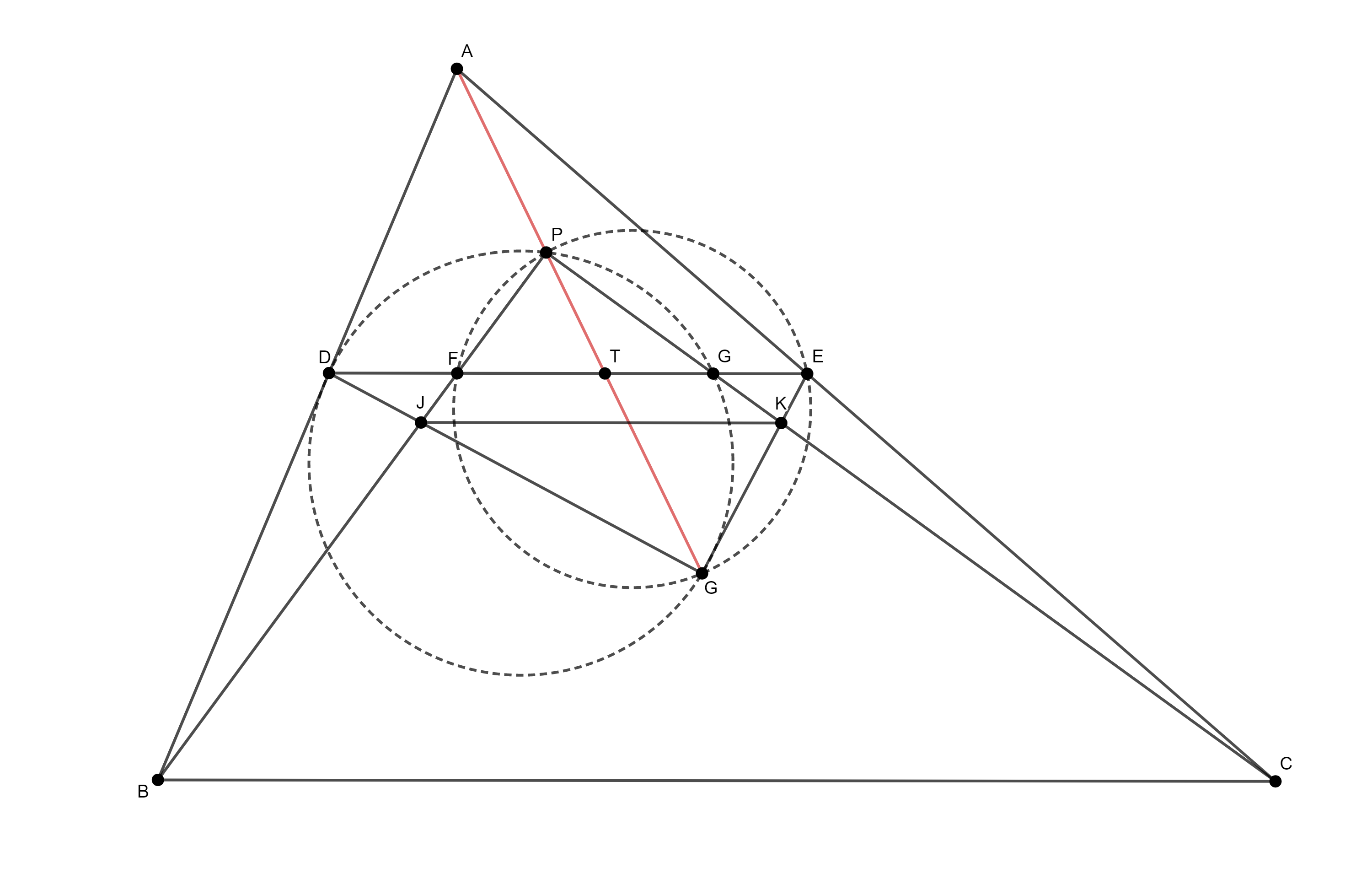
Рјешење: Означимо $J = DQ \cap BP$, $K = EQ \cap CP$. Уколико докажемо да je $JK||DE$, одатле ће слиједити да су троуглови $BDJ$ и $CEK$ перспективни у односу на центар, па ће према Дезарговој теореми бити и перспективни у односу на осу, што управо значи да су тачке $A$, $P$, $Q$ колинеарне.

Приступимо сада доказивању паралелности правих $JK$ и $DE$. Означимо $T = DE \cap PQ$. Примјеном Менелајеве теореме на троугао $DTQ$ и праву $PF$ добијамо: $\frac{DJ}{JQ}\cdot\frac{QP}{PT}\cdot\frac{TF}{FD}=-1$. Аналогно je из троугла $ETQ$ и праве $PG$: $\frac{EK}{KQ}\cdot\frac{QP}{PT}\cdot\frac{TQ}{QE}=-1$.

Дијељењем претходне двије једнакости, уз коришћење релације $DT\cdot TG=FT \cdot TE$ (што важи јер je тачка $T$ на радикалној оси кругова описаних око $\Delta DPG$ и $\Delta FPE$), добијамо: $\frac{DJ}{JQ}=\frac{EK}{KQ}$.

Одавде je $JK||DE$, па je и тврђење задатка у потпуности доказано.

Задатак 4: Дат je троугао $ABC$ и на страници $BC$ тачке $D$, $E$ тако да je $BD = DE = EC$. Права $p$ сијече дужи $AB$, $AD$, $AE$, $AC$ у тачкама $K$, $L$, $M$, $N$, редом. Доказати да je $KN \geq 3LM$.

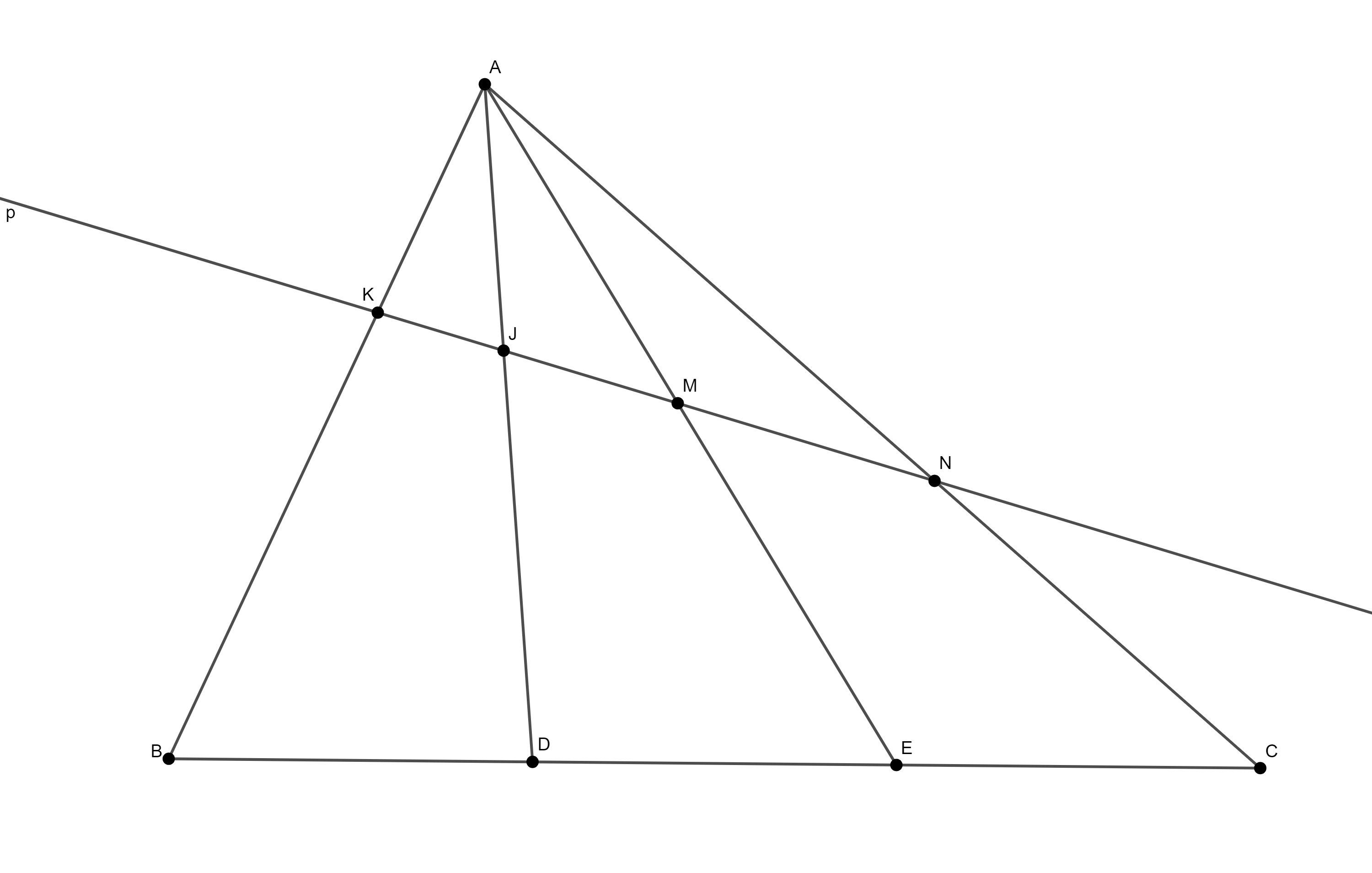
Рјешење: Означимо $x = KL$, $y = LM$, $z = MN$. Треба доказати да je $x+y +z \geq 3y$, односно $x+z \geq 2y$. Како je $R(K, N; L, M) = R(B, C; D, E)$, важи $$\frac{x}{y+z} : \frac{x+y}{z} = \frac{KL}{LN} : \frac{KM}{MN} = \frac{BD}{DC}:\frac{BE}{EC} = \frac{1}{2} :\frac{1}{2},$$ одакле je $4xz=(x+y)(y+z)$. Када би било $y>\frac{x+z}{2}$, било би $$x+y >\frac{3}{2}x+\frac{1}{2}z = 2\frac{1}{4}(x+x+x+z)\geq 2\sqrt[4]{xxxz}$$ и аналогно $y+z>2\sqrt[4]{xzzz}$, па и $(x + y)(y + z) > 4xz$, у супротности са ранијим закључком. Дакле, претпоставка $y>\frac{x+z}{2}$ je била погрешна, односно важи: $y\leq\frac{x+z}{2}$.

Испитајмо још када важи једнакост.
Ако je $y=\frac{x+z}{2}$, онда je $4xz = (x+ y)(x+ z) = \frac{(3x+z)(x+3z)}{4}$, што je еквивалентно са $(x − z)^2 = 0$. Дакле, једнакост важи ако je $x = y = z$ (ово је испуњено ако и само ако je $p||BC$).

Задатак 5: Дат je тетивни четвороугао $ABCD$. Праве $AB$ и $CD$ се сијеку у тачки $E$, a дијагонале $AC$ и $BD$ у тачки $F$. Описани кругови око троуглова $\Delta AFD$ и $\Delta BFC$ се сијеку поново у тачки $H$. Доказати да je $\angle EHF = 90^\circ$.

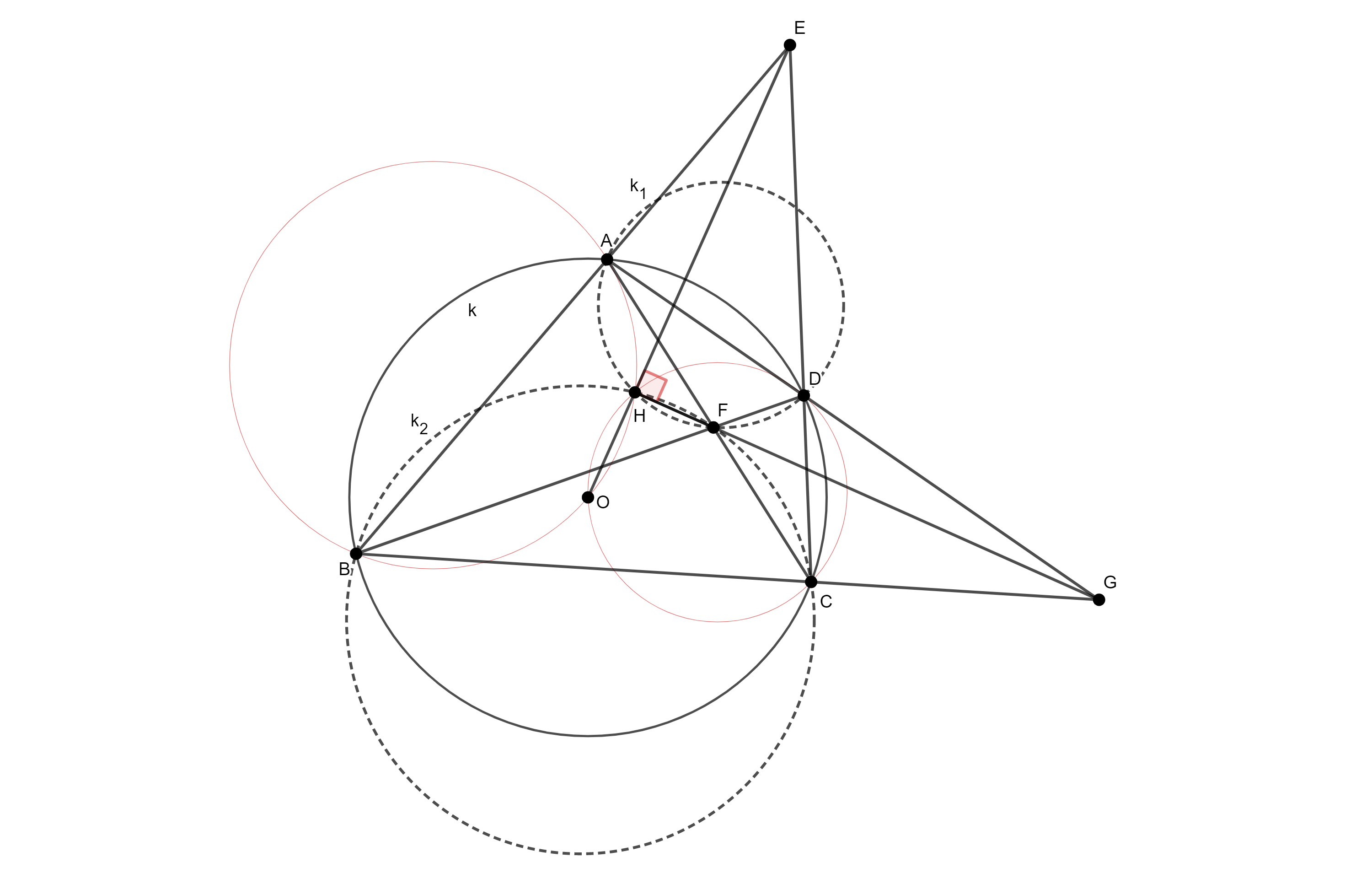
Рјешење: Означимо $G = AD \cap BC$. Означимо круг описан око четвороугла $ABCD$ са $k$, a кругове описане око троуглова $ADF$ и $BCF$ са $k_1$ и $k_2$, респективно. Примијетимо да je радикална оса кругова $k$ и $k_1$ права $AD$, кругова $k$ и $k_2$ права $BC$, кругова $k_1$ и $k_2$ права $FH$. Према познатој теореми, ове три радикалне осе се сијеку у једној тачки, која je управо тачка $G$. Другим ријечима, доказали смо да су тачке $F$, $G$, $H$ колинеарне. Без умањења општости, претпоставимо да je распоред тачака $B(G,F,H)$ (алтернативно, могу се у дањем доказу користити оријентисани углови). Користећи тетивне четвороуглове $ADFH$ и $BCFH$, добијамо $$\angle DHF = \angle DAF = \angle DAC \quad \text{и} \quad \angle FHC = \angle FBC = \angle DBC$$ па je $$\angle DHC = \angle DHF + \angle FHC = \angle DAC + \angle DBC = 2\angle DAC = \angle DOC.$$ Зато су тачке $D$, $C$, $H$ и $O$ коцикличне.
Слично се доказује и да су тачке $A$, $B$, $H$, $O$ коцикличне.
Означимо са $k_3$ и $k_4$ кругове описане око четвороуглова $ABHO$ и $DCHO$, респективно. Примијетимо да je радикална оса кругова $k$ и $k_3$ права $AB$, кругова $k$ и $k_2$ права $CD$, кругова $k_3$ и $k_4$ права $OH$. Радикалне осе ова три круга се сијеку у једној тачки, која je управо тачка $E$. Овим смо доказали да су тачке $O$, $H$, $E$ колинеарне.
Према Брокаровој теореми је $FH \bot OE$, што због $FH = GH$ и $OE = HE$ повлачи да је $GH \bot HE$, што је требало доказати.

Задатак 6: Око четвороугла $ABCD$ описана је кружница $k$. Праве $АВ$ и $СD$ се сијеку у тачки $Е$, те вриједи $АВ = ВЕ$. Пресјек тангенти у $В$ и $D$ на кружницу $k$ је тачка $F$. Ако су праве $АВ$ и $DF$ паралелне, доказати да су тачке $А$, $С$, $F$ колинеарне. (XXI Математичка олимпијада БиХ, Високо,14.5.2016)

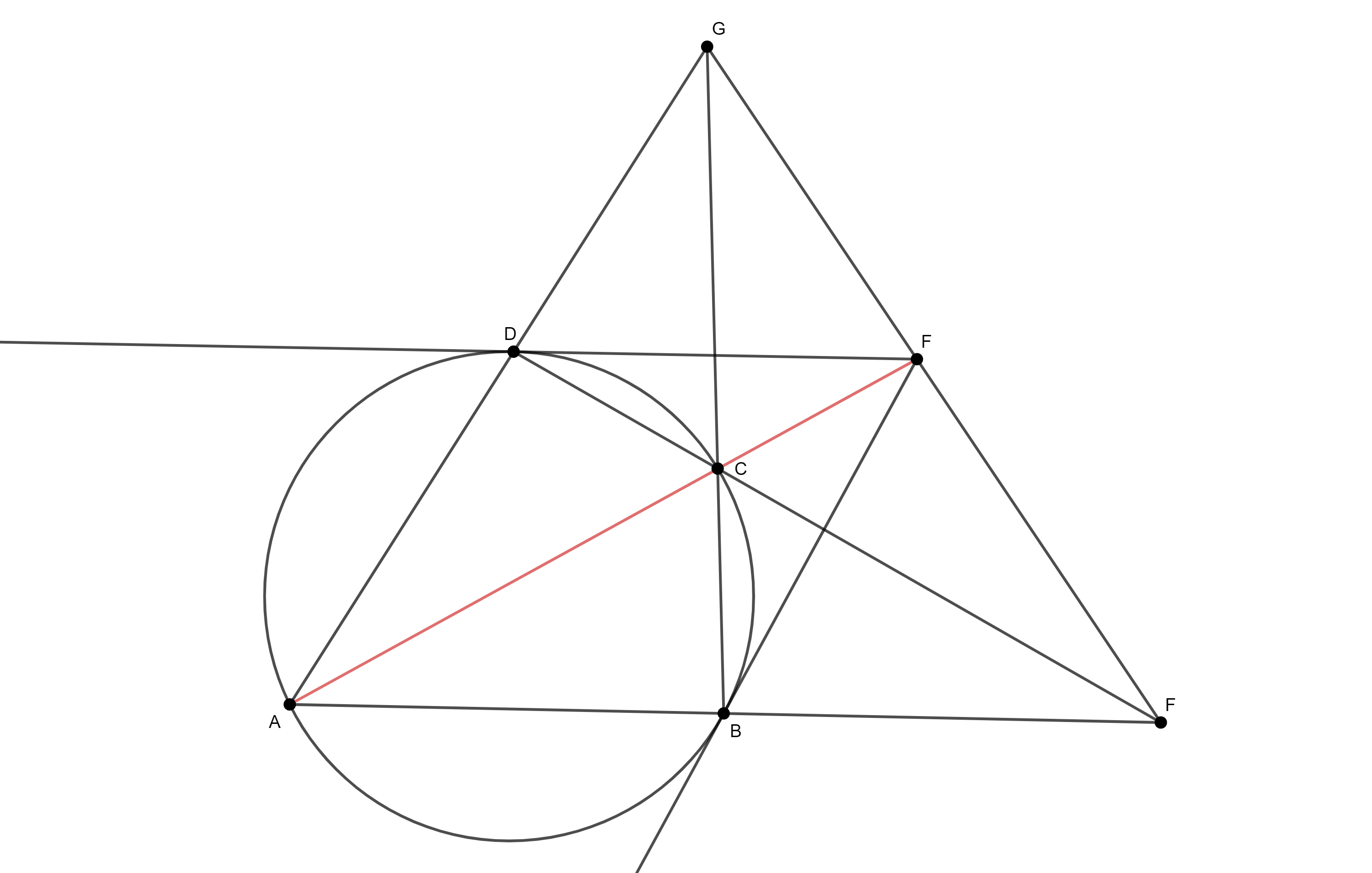
Рјешење: Из Паскалове теореме на (дегенерисани) шестоугао $ABBCDD$ имамо да се праве $AD$, $BC$ и $EF$ сијеку у једној тачки или су паралелне (јер је $E = AB \cap CD$ и $F = BB \cap DD$). Ако се сијеку у једној тачки, нека је то тачка $G$.

Да би $A$, $C$, $F$ биле колинеарне, довољно је доказати да се праве $AF$, $GB$ и $ED$ сијеку у једној тачки, тј. по Чевиној теореми да вриједи $\frac{AB}{BE}\cdot \frac{EF}{FG}\cdot\frac{GD}{DA} = 1$. Посљедња једнакост вриједи због $AB = BE$ и $\frac{GD}{AD}= \frac{FG}{FE}$ (Талесова теорема).

Задатак 7: Уписана кружница троугла $ABC$ додирује странице $BC$, $CA$, $AB$ у тачкама $D$, $E$, $F$ редом. Нека је $X$ тачка у троуглу $ABC$ таква да уписана кружница троугла $XBC$ додирује $BC$ у тачки $D$, и додирује $CX$ и $XB$ у тачкама $Y$ и $Z$ редом. Доказати да су тачке $E$, $F$, $Z$, $Y$ коцикличне. (Приједлог за Међународну математичку олимпијаду, 1995)

Рјешење: Најприје ћемо показати сљедећу лему: користимо већ наведене ознаке у задатку и означимо са $T$ тачку пресјека $EF$ и $ВС$. Тада је тачка $T$ хармонијски конјугована са тачком $D$ у односу на тачке $B$,$C$.

Нека је $P = EF \cap AD$. Тачка $T$ припада полари тачке $A$, па тачка $A$ припада полари тачке $T$. Такође, тачка $D$ припада полари тачке $T$, па закључујемо да је $AD$ полара тачке $T$ (у односу на уписани круг троугла $ABC$). Како $P \in TEF$ и $P$ припада полари тачке $T$, то значи да вриједи $(T, P; F,E) = -1$. Међутим, вриједи и $(T, P; F,E) = (T, D; B, C)$ па закључујемо да вриједи $(T, D; B, C) = -1$. Овим је лема доказана.

Сада, ако примијенимо горе наведену лему на $ABC$ и $XBC$ и ако је $T = EF \cap BC$ и $T’ = YZ \cap BC$ добијамо да обје тачке и $T$ и $T’$ морају бити хармонијски конјуговане се тачком $D$, па вриједи $T\equiv T’$ Коначно, вриједи $TE \cdot TF = TD^2 = TY\cdot TZ$ одакле слиједи да је четвороугао $EFZY$ тетиван, што је и требало доказати.

Задатак 8: Нека је $k$ описана кружница око оштроуглог троугла $ABC$ и $H$ ортоцентар датог троугла. Нека је $D = BH \cap AC$ и $E = CH \cap AB$. Кружница описана око троугла $ADE$ сијече поново кружницу $k$ у тачки $F$. Доказати да се симетрале углова $BHC$ и $BFC$ сијеку на страници $BC$. (Бразилска математичка олимпијада, 2011)

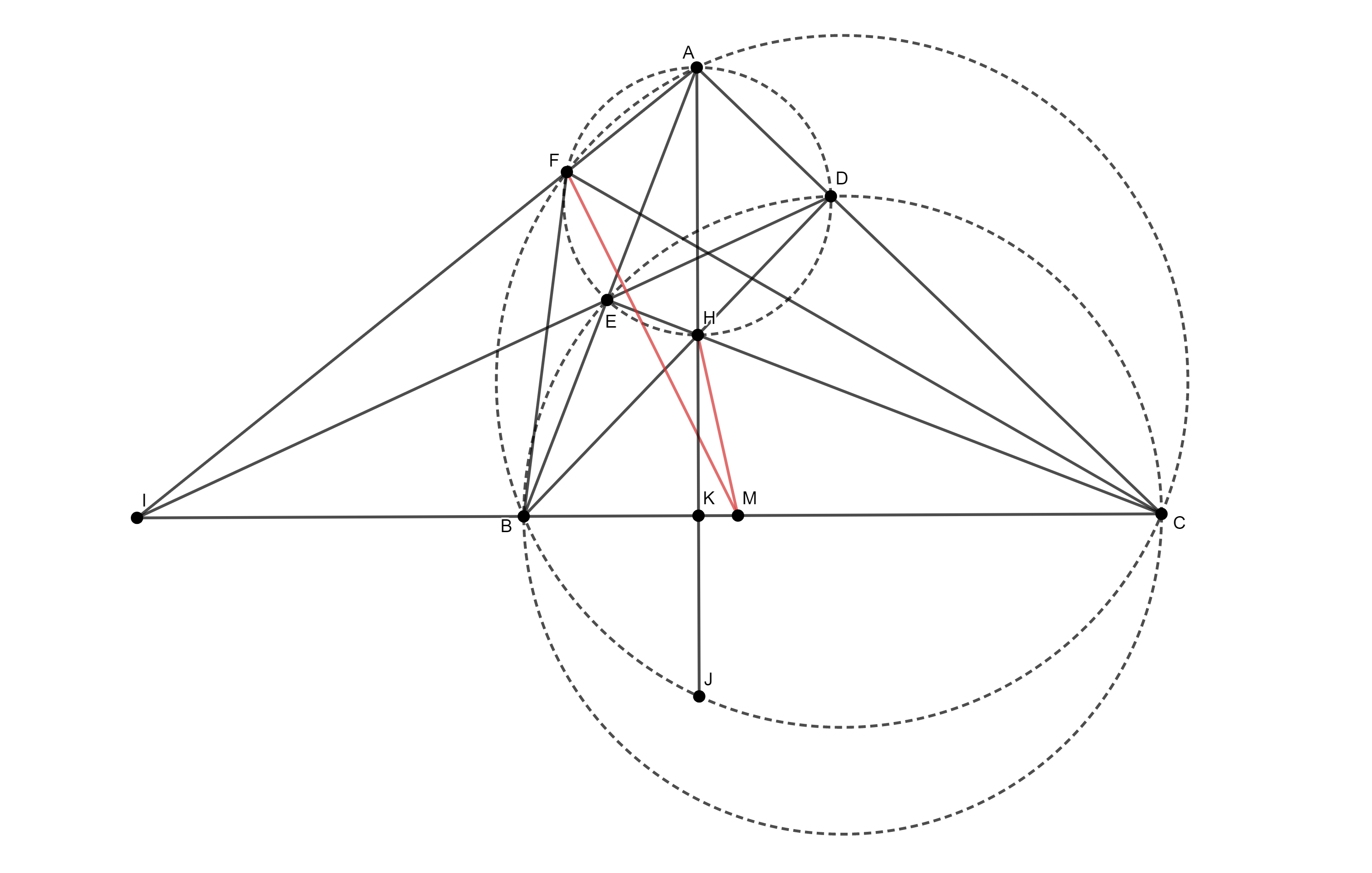
Рјешење: Нека је $J$ тачка симетрична тачки $H$ у односу на праву $BC$. Уведимо и сљедеће ознаке: $k_1$ – кружница описана око троугла $ADE$, $K = BC \cap AH$. Најприје ћемо доказати да је $BJCF$ хармонијски четвороугао.

Конструишимо кружницу $k_2$ над пречником $BC$. Тада вриједи: $AF$ је радикална оса кружница $k$ и $k_1$, $BC$ радикална оса кружница $k$ и $k_2$ и $DE$ радикална оса кружница $k_1$ и $k_2$. Сада на основу теореме о радикалним осама имамо да се праве $AF$, $BC$, $DE$ сијеку у једној тачки. Нека је то тачка $I$. Сада вриједи: $$-1 = (I,K;B,C)\stackrel{A}{=}(F,J;B,C)$$ одакле слиједи да је $BJCF$ хармонијски четвороугао.

Одавде слиједи: $\frac{BF}{JB} = \frac{FC}{CJ}$ a како је $BJ = BH$ и $CJ = CH$ (јер су троугао $BHC$ и $BJC$ подударни на основу става УСУ) имамо да вриједи: $$\frac{BF}{HB} = \frac{FC}{CH} \quad \text{тј.} \quad \frac{BF}{FC}=\frac{BH}{CH}.$$ Нека симетрала угла $BHC$ сијече $BC$ у тачки $M$, а симетрала угла $BFC$ у тачки $M^*$. На основу теореме о симетрали угла вриједи: $$\frac{BF}{FC} = \frac{BM^*}{CM^*}\quad \text{и} \quad \frac{BH}{CH}=\frac{BM}{CM}.$$ На основу претходних запажања слиједи $\frac{BM}{CM} = \frac{BM^*}{CM^*}$, а одавде је $M \equiv M^*$. Дакле, симетрале углова $BHC$ и $BFC$ се сијеку на страници $BC$, што је и требало показати.

Задатак 9: Нека је $ABCD$ конвексан четвороугао. Нека је $E = AB \cap CD$ и $F = AD \cap BC$ и $P$ тачка пресјека дијагонала. Нека је $O$ подножје нормале из $P$ на $EF$. Доказати да је $\angle BOC = \angle AOD$. (Кинеска математичка олимпијада, 2002)


Рјешење:

Лема: Нека тачке $B$, $M$, $C$, $N$ леже на једној правој у том поретку и нека је тачка $A$ ван те праве. Тада било која два од доље наведених услова имплицирају трећи:

• $H(B, C; M, N) = -1$
• $AM$ је симетрала угла $\angle BAC$
• $AM \bot AN$

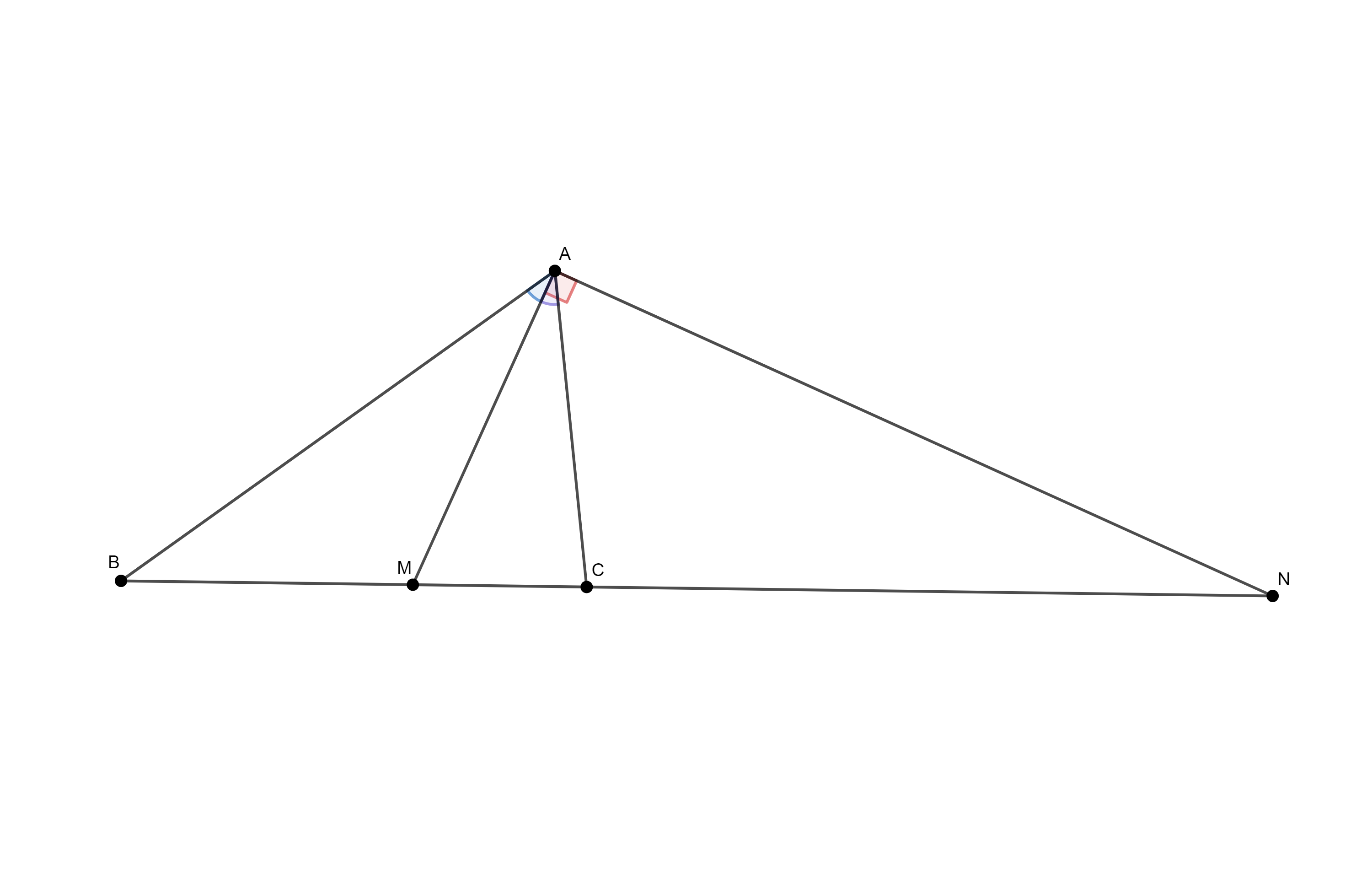
Доказ леме:
Означимо $\alpha = \angle BAC$, $\beta = \angle CBA$, $\gamma = \angle ACB$ и $\varphi = \angle BAM$. Примјеном синусне теореме на троуглове $\Delta ABM$ и $\Delta ACM$ добијамо $$\frac{BM}{MC} = \frac{BM}{AM}\cdot\frac{AM}{CM}=\frac{\sin\varphi}{\sin\beta}\cdot\frac{\sin\gamma}{\sin (\alpha-\varphi)}.$$ Слично, примјеном синусне теореме на троуглове $\Delta ABN$ и $\Delta ACN$ добијамо $$\frac{BN}{NC} = \frac{BN}{AN}\cdot\frac{AN}{CN} = \frac{\sin (90^\circ - \varphi)}{\sin (180^\circ-\beta)}\cdot\frac{\sin \gamma}{\sin (90^\circ +\alpha-\varphi)}.$$ Комбинујући претходне једначине, добијамо $$\frac{BM}{MC}:\frac{BN}{NC} = \frac{\tan \varphi}{\tan (\alpha- \varphi)}.$$
Дакле, $R(B, C; M, N) = -1$ je еквивалентно са $\tan \varphi = \tan (\alpha-\varphi)$, односно са $\varphi = \frac{\alpha}{2}$, па je овим тврђење доказанo.

Вратимо се сада на задатак.

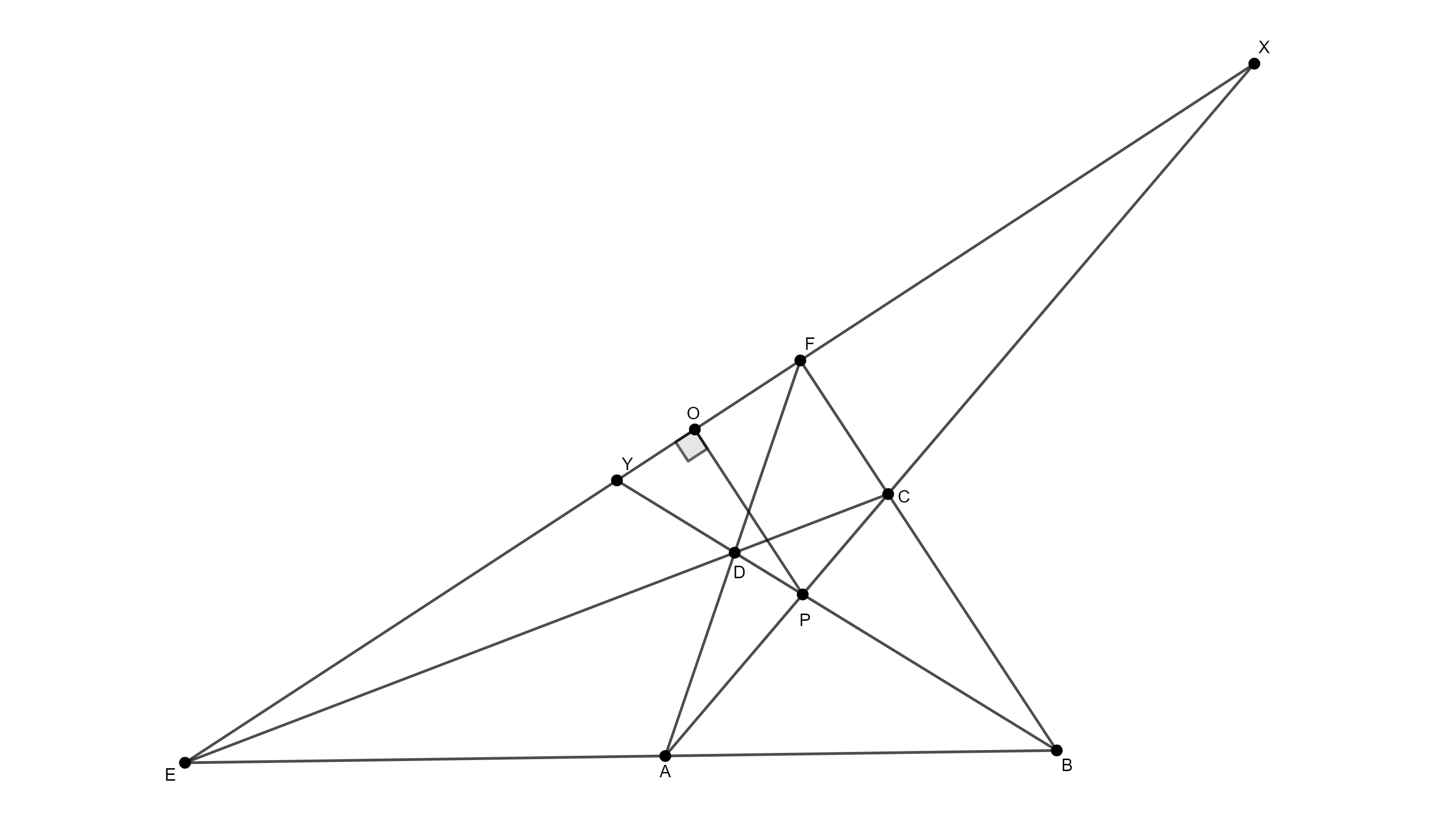
Нека су тачке $X$ и $Y$ пресјеци правих $AC$ и $BD$ са $EF$ редом. Праве $DY$, $EA$ и $FC$ се сијеку у тачки $B$, а тачке $A$, $C$ и $X$ су колинеарне.
Стога можемо примијенити редом Чевину и Менелајеву теорему на троугао $FDE$. Имамо сљедеће релације: $$\frac{EY}{YF} \cdot \frac{FA}{AD} \cdot \frac{DC}{CE} = 1 \quad \text{и} \quad \frac{FX}{XE}\cdot\frac{EC}{CD}\cdot\frac{DA}{AF} = -1.$$ Одавде добијамо да вриједи: $\frac{FX}{XE} = -\frac{FY}{YE}$, тј. $H(F, E; X, Y) = -1$. Дакле, тачке $F$, $E$, $X$, $Y$ су хармонијски спрегнуте. Са друге стране вриједи: $$-1 = (F, Е; X, Y) \stackrel{B}{=} (C, A; X, P) \quad \text{и} \quad -1 = (F, Е; X, Y) \stackrel{A}{=}(D, B; P, Y).$$ Дакле, имамо још два хармонијска спрега $H(C, A; X, P)$ и $H(D, B; P, Y)$ и вриједи из услова задатка да је $OP \bot EF$.
Сада на основу горе наведене леме закључујемо да вриједи $\angle AOP = \angle COP$ и $\angle BOP = \angle DOP$. Koначно, рачунањем углова добијамо: $$\angle BOC = \angle COP - \angle BOP = \angle AOP - \angle DOP = \angle AOD$$ што је и требало доказати.

Задатак 10: Taчке $P$ и $Q$ су на страници $BC$ оштроуглог троугла $ABC$ такве да је $\angle PAB = \angle BCA$ и $\angle CAQ = \angle ABC$. Тачке $M$ и $N$ се налазе на $AP$ и $AQ$ редом, такве да је тачка $P$ средиште $AM$, а тачка $Q$ средиште $AN$. Доказати да се праве $CN$ и $BM$ сијеку на кругу описаном око троугла $ABC$. (Међународна математичка олимпијада, 2014)

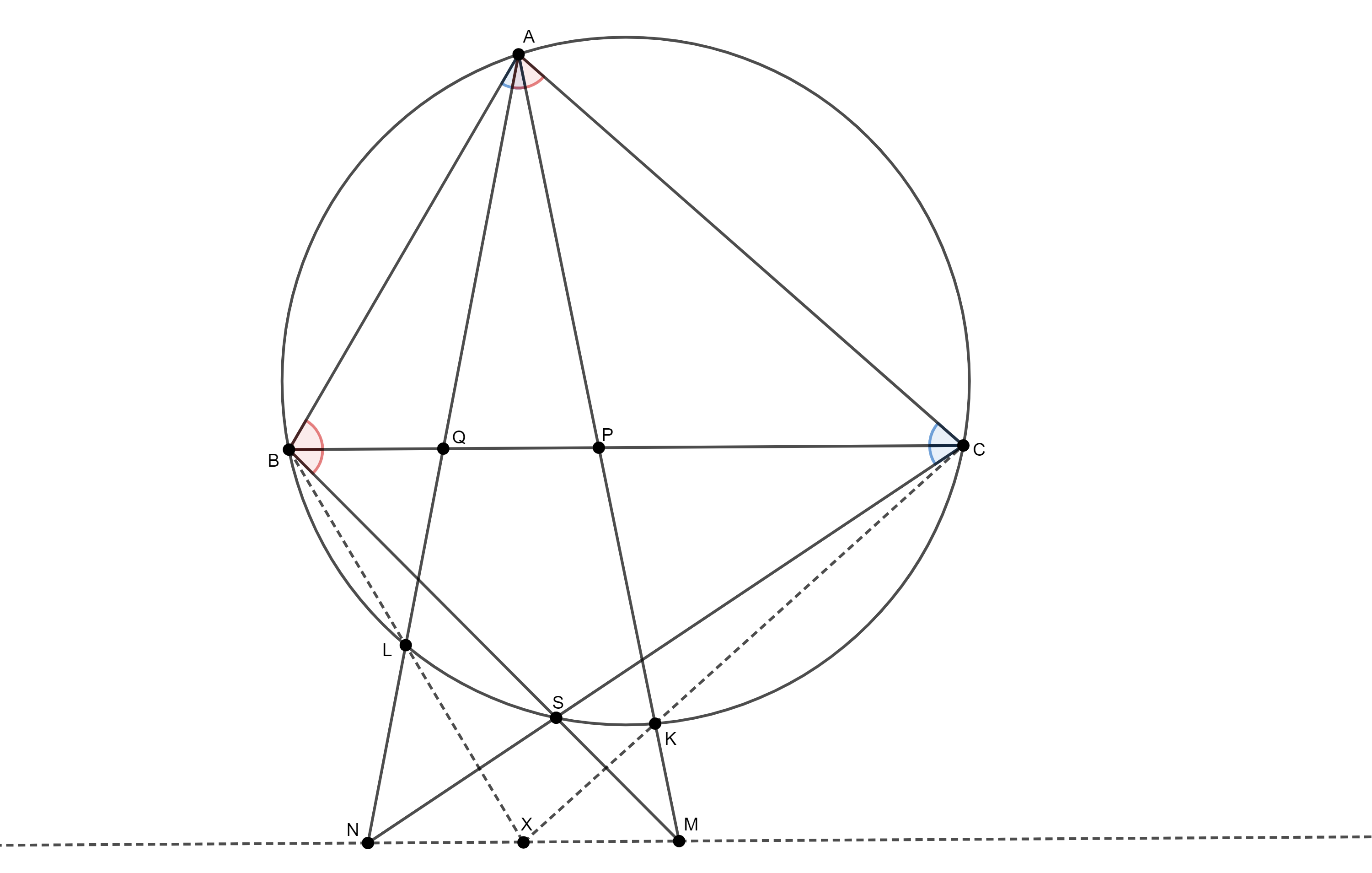
Рјешење 1: Нека је $S$ тачка пресјека правих $BM$ и $CN$. Даље, нека праве $AP$ и $AQ$ сијеку кружницу описану око троугла $ABC$ у тачкама $K$ и $L$, редом. Примијетимо да вриједи $\angle LBC = \angle LAC = \angle CBA$ и $\angle KCB = \angle KAB = \angle BCA$. Одавде слиједи да се праве $BL$ и $CK$ сијеку у тачки $X$, која је симетрична тачки $А$ у односу на праву $ВС$. Како је $AP = PM$ и $AQ = QN$, слиједи да тачка $X$ припада правој $MN$. Коначно, ако примијенимо Паскалову теорему на шестоугао $ALBSCK$, добијамо да тачка $S$ припада кружници описаној око троугла $ABC$, што је и требало доказати.

Рјешење 2: Нека се тангенте на кружницу описану око троугла $ABC$ у тачкама $B$ и $C$ сијеку у тачки $X$. Очигледно вриједи: $$\angle APB = 180^\circ - \angle ABC - \angle PAB = 180^\circ - \angle ABC - \angle BCA = 180^\circ - \beta - \gamma = \alpha.$$ Са друге стране, на основу теореме о углу између тангенте и тетиве вриједи $\angle XBC = \angle BAC = \alpha$. Па како је $\angle APB = \alpha = \angle XBP$ слиједи $XB||AP$. Аналогно, добијамо да вриједи и $XC||AQ$. Нека сада праве $BM$ и $CN$ сијеку кружницу описану око троугла $АВС$ у тачкама $S_1$ и $S_2$, редом. Уведимо још двије тачке у бесконачности $P_{\infty}\in AP$ и $Q_{\infty}\in AQ$. Имамо да вриједи: $$1 = (A, M; P, Р_{\infty}) \stackrel{B}{=}_k (A, S_1; C, B) \quad \text{и} \quad 1 = (A, N; Q, Q_{\infty})\stackrel{B}{=}_k (A, S_2; B, C).$$ Одавде закључујемо $S_1 \equiv S_2 \equiv S$, тј. четвороугао $ABSC$ је хармонијски, па слиједи да се праве $СN$ и $ВМ$ сијеку на кругу описаном око троугла $ABC$, што је и требало доказати.