Пројективна геометрија
Почетна страна»
Увод»
Дворазмјера. Хармонијска спрегнутост. Перспективитет. Пројективитет»
Дезаргова теорема»
Папасова и Паскалова теорема»
Пол и полара. Конјуговане тачке»
Бријаншонова и Брокарова теорема»
Задаци»
Литература»
Стефан Малбашић,
Универзитет у Београду, Математички факултет
Дезаргова теорема.
Троуглови $A_1B_1C_1$ и $A_2B_2C_2$ су перспективни у односу на центар ако праве $A_1A_2$, $B_1B_2$ и $C_1C_2$ припадају једном прамену, a перспективни у односу на осу ако су тачке $X = A_1B_1 \cap A_2B_2$, $Y = B_1C_1 \cap B_2C_2$, $Z = A_1C_1 \cap A_2C_2$ колинеарне.
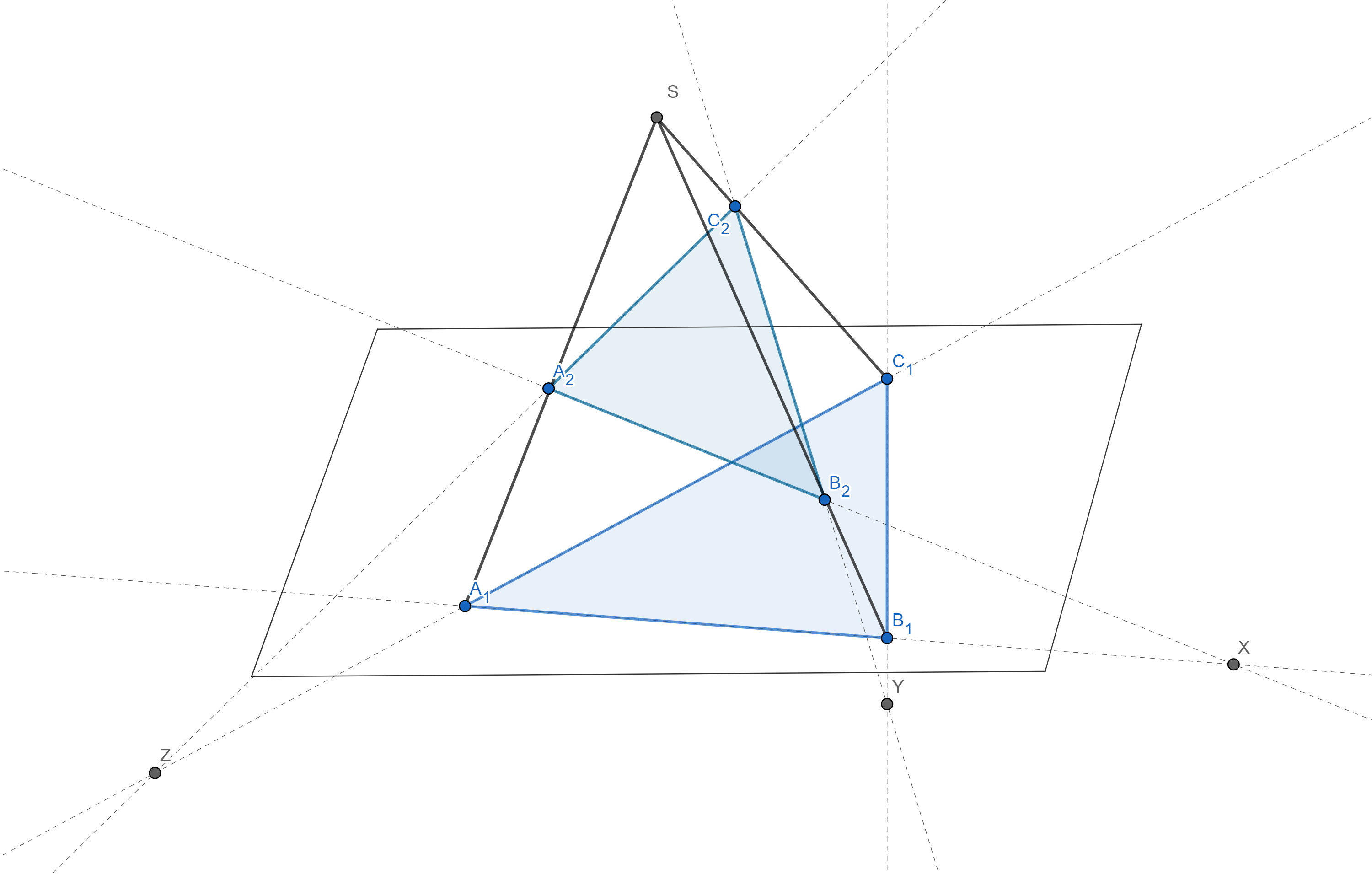
Дезаргова теорема: Два троугла су перспективна у односу на центар ако и само ако су перспективни у односу на осу.
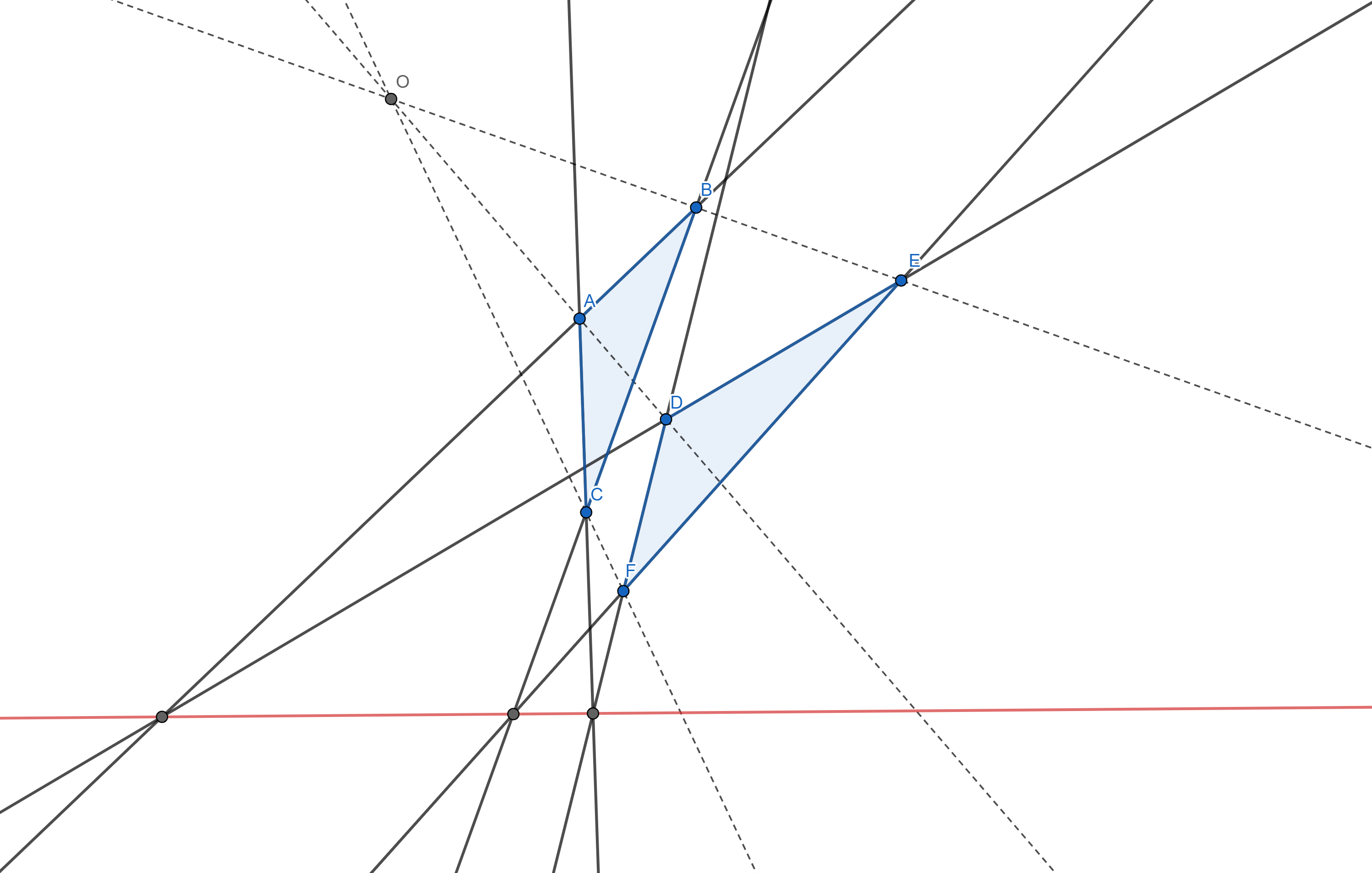
Обрат Дезаргове теореме: Ако пресјечне тачке парова одговарајућих страница двају троуглова или правих које садрже те странице, припадају једној правој, тада се праве које спајају парове одговарајућих тјемена троуглова сијеку у једној тачки.
