Пројективна геометрија
Почетна страна»
Увод»
Дворазмјера. Хармонијска спрегнутост. Перспективитет. Пројективитет»
Дезаргова теорема»
Папасова и Паскалова теорема»
Пол и полара. Конјуговане тачке»
Бријаншонова и Брокарова теорема»
Задаци»
Литература»
Стефан Малбашић,
Универзитет у Београду, Математички факултет
Пол и полара. Конјуговане тачке.
Нека je дат круг $k(O, r)$. За тачку $P \neq O$ у равни, означимо са $P^*$ инверзну слику тачке $P$ у односу на круг $k$ (тј. тачку на полуправој $OP$ за коју је испуњено $OP^* \cdot OP = r_2$).
Дефиниција. Полара тачке $P$ у односу на круг $k$ je права $p$ кроз $P^*$ нормална на $OP^*$. Обрнуто, тачка $P$ je пол праве $p$.
Специјално, ако je тачка $P$ ван круга $k$, њена полара je права $MN$, гдје су $M$ и $N$ додирне тачке тангенти из $P$ на $k$.
Дефиниција. Пресликавање које сваку тачку слика у њену полару, а сваку праву у њен пол, зове се поларно пресликавање.
Поларно пресликавање је бијекција између скупа тачака и скупа правих у пројективној равни. Полара тачке $О$ је бесконачна права, а полови правих кроз $О$ су бесконачне тачке.
Сљедеће тврђење нам показује да поларно пресликавање чува инциденцију. Убрзо ће се испоставити да је то својство од кључне важности.
Теорема 4. Ако тачка $Р$ лежи на полари тачке $Q$ у односу на круг $k$, онда и тачка $Q$ лежи на полари тачке $Р$.
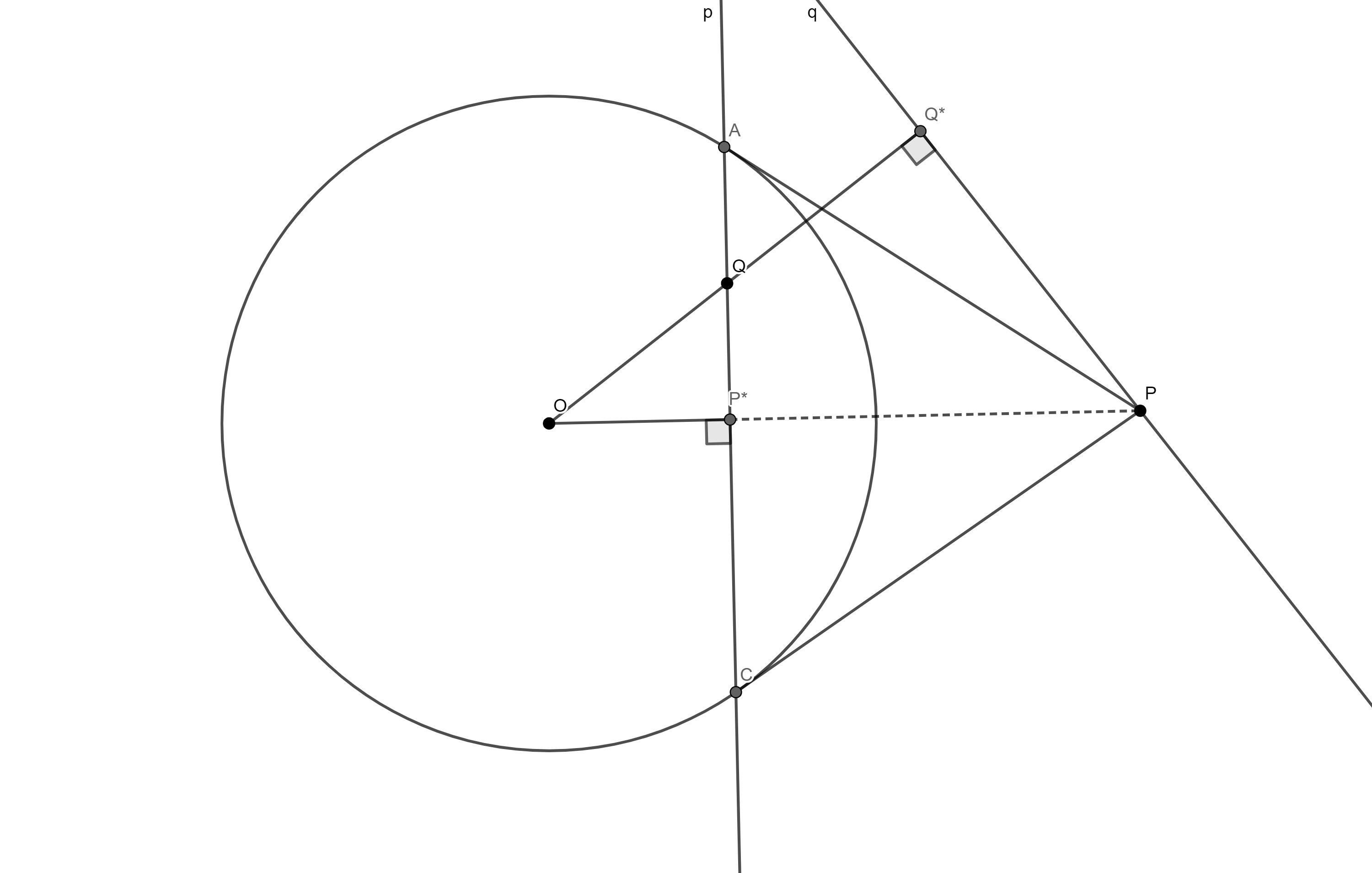
Доказ: Троуглови $\Delta OQ^*P$ и $\Delta OP^*Q$ су слични. Ако je $P$ на полари тачке $Q$, по дефиницији je $\angle OQ^*P = 90^\circ$, a тада je и $\angle OP^*Q = 90^\circ$, тј. $Q$ je на полари тачке $P$. $\square$
Значај ових појмова се најзад огледа у сљедећој теореми.
Теорема 5. Нека су $A$, $B$, $C$ и $D$ тачке на кругу $k$. Ако се праве $AB$ и $CD$ сијеку у $E$, $BC$ и $AD$ у $F$, и $AC$ и $BD$ у $G$, онда je $EF$ полара тачке $G$ (у односу на $k$).
Доказ: Означимо са $M$ пресјек тангенти на $k$ у тачкама $A$ и $C$, и са $N$ пресјек тангенти у $B$ и $D$. Поларе тачака $M$ и $N$ су праве $AC$ и $BD$ редом, и те праве садрже $G$, па на основу T.4 тачке $M$ и $N$ леже на полари тачке $G$. Слиједи да je $MN$ полара тачке $G$. Међутим, по посљедици Паскалове теореме, тачке $E$ и $F$ леже на правој $MN$. $\square$
Дефиниција. Тачке $A$ и $B$ називамо конјугованим у односу на круг $k$ ако једна од њих лежи на полари друге.
Teorema 6. Ако права одређена двјема конјугованим тачкама $A$ и $B$ сијече круг $k(O, r)$ у тачкама $C$ и $D$, онда je $H(A, B; C, D)$. Обратно, ако важи $H(A, B; C, D)$, при чему $C$ и $D$ леже на кругу $k$, онда су $A$ и $B$ конјуговане у односу на круг $k$.
Доказ: Нека су $C_1$, $D_1$ пресјечне тачке $OA$ са кругом $k$. Како инверзија чува дворазмјеру, важи $R(C_1, D_1; A, А^* ) = R(C_1, D_1; A^*, A)$, па je $$H(C_1,D_1;A,A^*).$$ Нека je сада $p$ права која садржи тачку $A$ и сијече круг $k$ у тачкама $C$ и $D$. Нека je $E = CC_1 \cap DD_1$, $F = CD_1 \cap DC_1$. Како je $C_1D_1$ пречник круга $k$, важи $C_1F \bot D_1E$ и $D_1F \bot C_1E$, па je $F$ ортоцентар троугла $C_1D_1E$. Нека je $B = EF \cap CD$ и $\overline{A^*}= EF \cap C_1D_1$. Због $$C_1D_1A\overline{A^*} \stackrel{E}{=} CDAB \stackrel{F}{=} D_1C_1A\overline{A^*}$$ имамо да је $H(C_1, D_1; A, \overline{A^*})$ и $H(C, D; A, B)$. Одавде, због $H(C_1,D_1;A,A^*)$, закључујемо двије ствари:
Прво, из $H(C_1, D_1; A, \overline{A^*})$ и $H(C_1, D_1; A, A^*)$ слиједи $A^* = \overline{A^*}$, па je $A^* \in EF$, a како je и $EF \bot C_1D_1$, права $EF = a$ je полара тачке $A$.
Друго, за тачку $B$ која, како смо управо видјели, припада полари тачке $A$ важи $H(C, D; A, B)$. Овим је теорема доказана. $\square$
