Стефан Малбашић,
Универзитет у Београду, Математички факултет

Папасова и Паскалова теорема.

Папасова теорема: Нека се тачке $A_1$, $A_2$, $A_3$ налазе на правој $a$, a тачке $B_1$, $B_2$, $B_3$ на правој $b$. Нека je $A_1B_2 \cap A_2B_1 = C_3$, $A_1B_3 \cap A_3B_1 = C_2$, $A_2B_3 \cap A_3B_2 = C_1$. Тада су $C_1$, $C_2$, $C_3$ колинеарне.

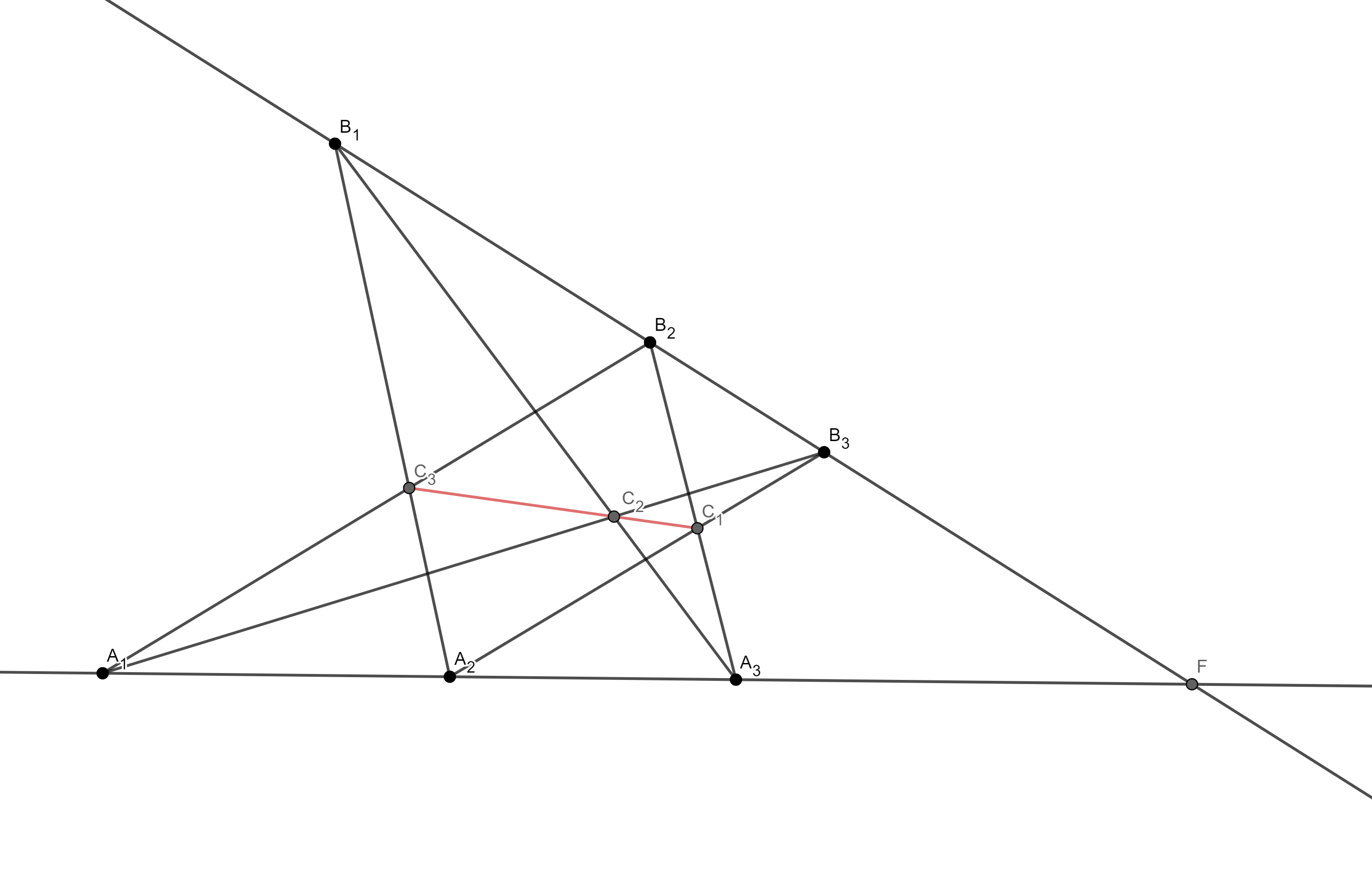
Доказ: Означимо са $C’_2 = C_1C_3 \cap A_3B_1$, $D = A_1B_2 \cap A_3B_1$, $E = A_2B_1 \cap A_3B_2$ и са $F = a \cap b$. Наш циљ je да докажемо да су тачке $C_2$ и $C’_2$ идентичне. Уочимо низ пројективитета: $$A_3B_1DC_2 \stackrel{A_1}{=} FB_1B_2B_3 \stackrel{A_2}{=} A_3EB_2C_1 \stackrel{C_3}{=} A_3B_1D C’_2.$$ На тај начин смо добили пројективно пресликавање праве $A_3B_1$ при ком су фиксне тачке $A_3$, $B_1$, $D$, a тачка $C_2$ се пресликава у тачку $C’_2$. Како je пројективно пресликавање са три фиксне тачке идентичко пресликавање, слиједи да je $C_2 = C’_2$. $\square$

Паскалова теорема: Нека су $A$, $B$, $C$, $D$, $E$, $F$ тачке на кругу. Праве $AB$ и $DE$ сијеку се у $L$, праве $BC$ и $EF$ у $M$, a $CD$ и $FA$ у $N$. Тада су тачке $L$, $M$, $N$ колинеарне.

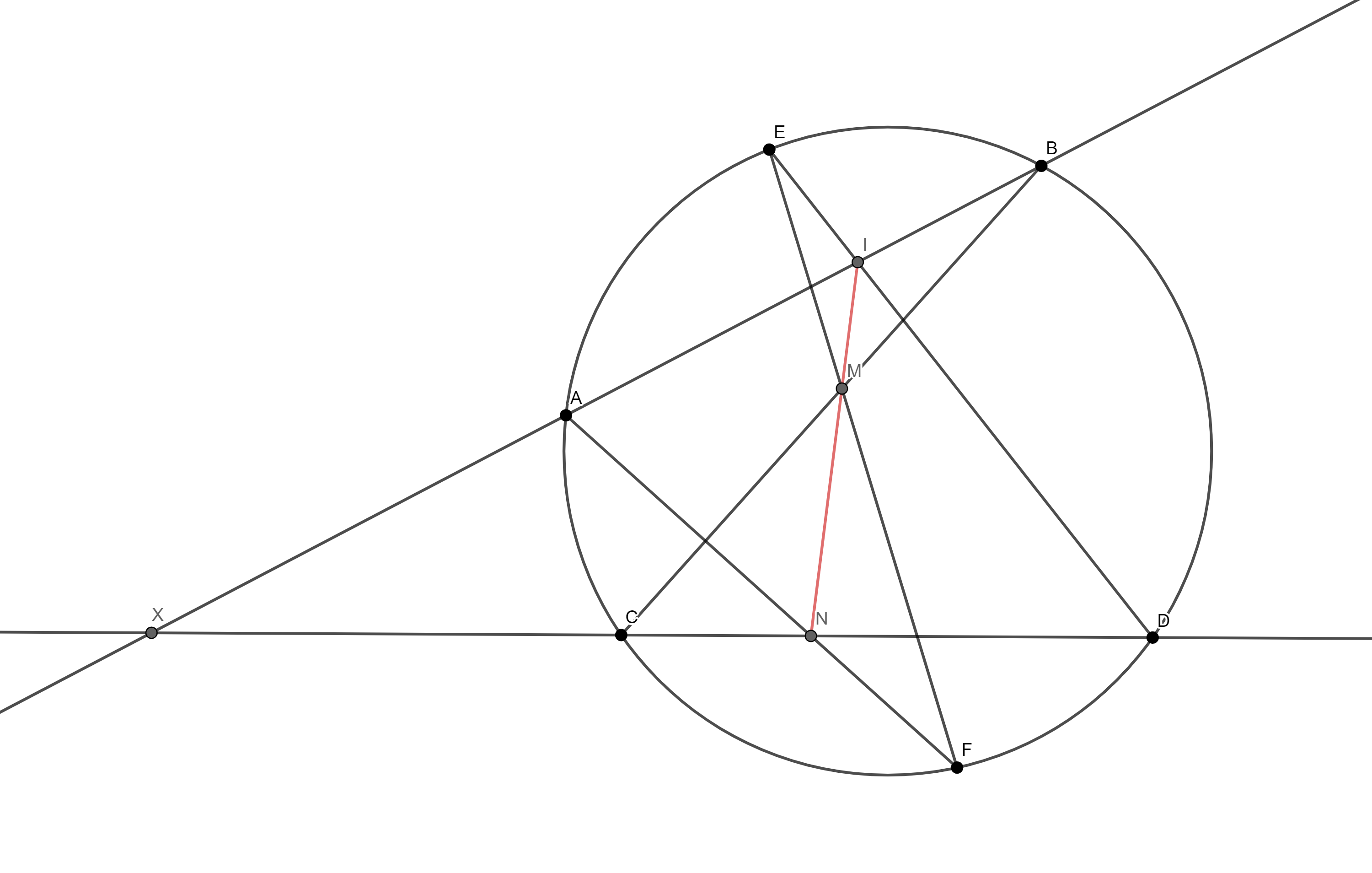
Доказ: Све дужи у овом доказу су оријентисане. Нека се $AB$ и $CD$ сијеку у $X$, $CD$ и $EF$ у $Y$, a $EF$ и $AB$ у $Z$. Тачке $L$, $M$, $N$ леже на правим које садрже странице троугла $XYZ$, па можемо да примијенимо Менелајеву теорему: треба показати да је $\frac{ZL}{LX}\cdot \frac{XN}{NY}\cdot\frac{YM}{MZ}=-1$. Радимо са $\Delta XYZ$ као базним троуглом. Знамо да су тачке $L$, $D$, $E$ на правој, па Менелајева теорема даје $\frac{XD}{DY} \cdot \frac{YE}{EZ} \cdot \frac{ZL}{LX} = -1$. И тачке $C$, $M$, $B$ су колинеарне, па имамо и $\frac{XC}{CY} \cdot \frac{YM}{MZ} \cdot \frac{ZB}{BX} = -1$. Најзад, тачке $N$, $F$, $A$ су колинеарне, па je $\frac{XN}{NY} \cdot \frac{YF}{FZ} \cdot \frac{ZA}{AX} =-1$. Множењем ове три једнакости, користећи и једнакост потенције: $$XD \cdot XC = XB \cdot XA, \quad YD \cdot YC = YF \cdot YE, \quad ZF \cdot ZE = ZB \cdot ZA,$$ добијамо оно што нам је потребно. $\square$

Паскалова теорема очигледно не захтијева да $ABCDEF$ буде конвексан шестоугао, тако да су сви распореди тачака дозвољени.

Напомена: Можемо да посматрамо и дегенерисане случајеве, када су неке двије праве паралелне или се неке двије тачке поклапају. На примјер, ако је $A = B$, за праву $AB$ узимамо тангенту на круг у тачки $A$.

Доказ Паскалове теореме употребом пројективне геометрије:
Нека су $A_1$, $A_2$, $A_3$, $B_1$, $B_2$, $B_3$ коцикличне тачке. Тачке добијене у пресјецима $A_1B_2$ са $A_2B_1$, $A_1B_3$ са $A_3B_1$, $A_2B_3$ са $A_3B_2$ леже на једној правој.

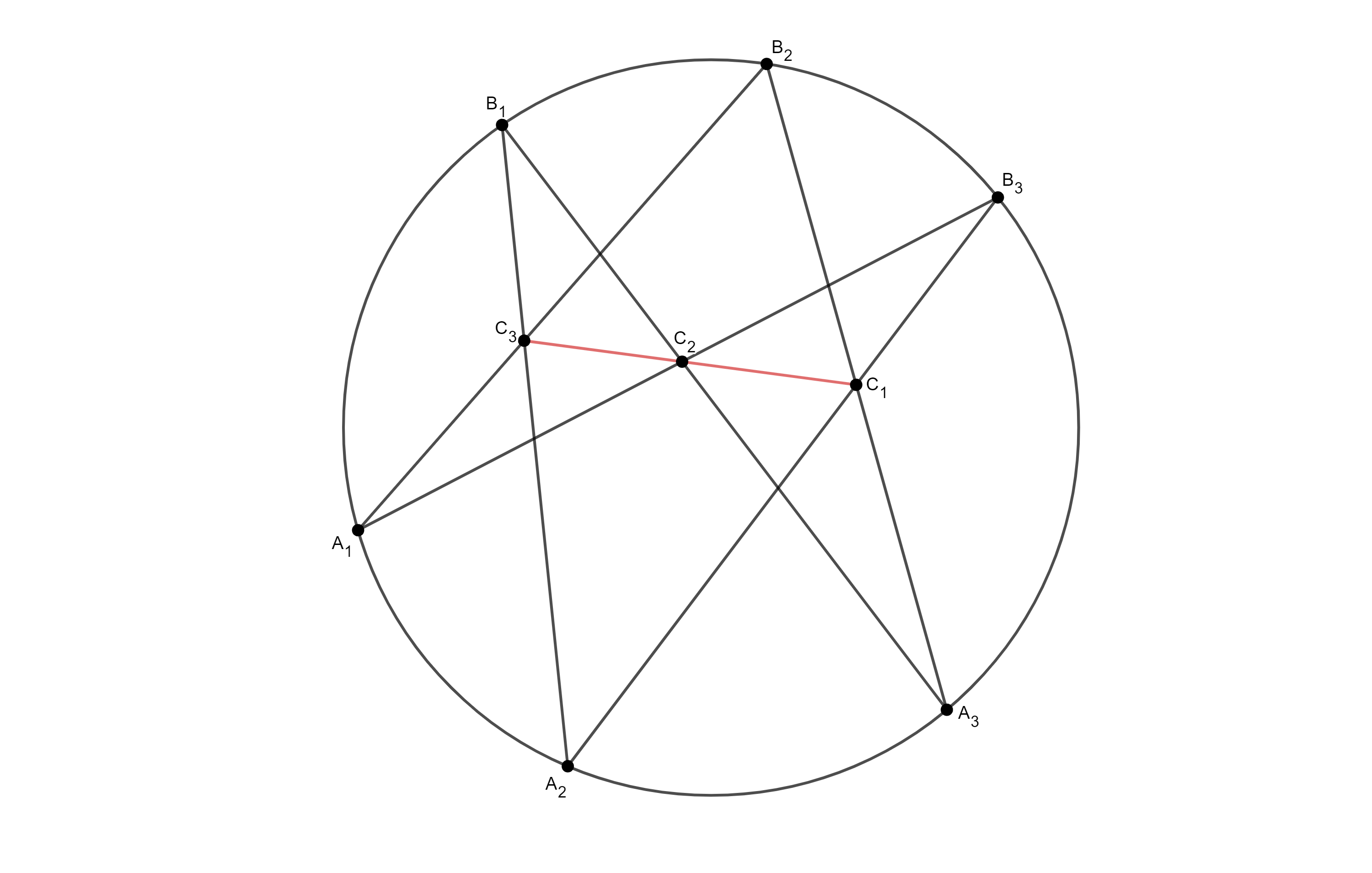
Означимо $C'_2 = C_1C_3 \cap A_3B_1$, $D = A_1B_2 \cap A_3B_1$, $E = A_2B_1 \cap A_3B_2$ (аналогно Папасовој теореми). Затим уочимо низ пројективитета $$A_3B_1DC_2 \stackrel{A_1}{=} A_3B_1B_2B_3 \stackrel{A_2}{=} A_3EB_2C_1 \stackrel{C_3}{=} A_3B_1DC'_2,$$ и на исти начин закључујемо да је $C_2 = C'_2$. $\square$

Теорема 3. У тетивном четвороуглу $ABCD$, праве $AB$ и $CD$ се сијеку у $E$, $BC$ и $DA$ у $F$. Тангенте на описани круг у тачкама $A$ и $C$ се сијеку у $P$, a тангенте у $B$ и $D$ се сијеку у $Q$. Тада тачке $E$, $F$, $P$ и $Q$ леже на истој правој.

Доказ: Примијенићемо Паскалову теорему на дегенерисани шестоугао $AABCCD$. Тачке $E =AB \cap CD$, $F = BC \cap DA$ и $P = AA \cap CC$ су колинеарне. Аналогно, и $Q$ припада тој правој. $\square$

Такође, будући да је Паскалова теорема тврђење из пројективне геометрије, треба да будемо спремни и на бесконачне тачке. Све бесконачне тачке леже на тзв. бесконачној правој.

Примјер. Дате су тачке $A$, $B$, $C$, $D$, $E$, $F$ на кругу. Ако је $AB||DE$ и $BC||EF$, доказати да је онда и $CD||FA$.

Доказ: На основу Паскалове теореме, тачке $AB \cap DE$, $BC \cap EF$ и $CD \cap FA$ леже на истој правој. Међутим, како су праве двије пресјечне тачке бесконачне, то мора бити бесконачна права. Дакле, и трећа пресјечна тачка $CD \cap FA$ је бесконачна, тј. $CD||FA$. $\square$